题目内容
某校七年级运动队为了备战校运动会需要购置一批运动鞋.已知该队伍有20名同学,统计表如下表.由于不小心弄脏了表格,有两个数据看不到.
| 鞋码 | 38 | 39 | 40 | 41 | 42 |
| 人数 | 5 | 3 | 2 |
- A.中位数是40,众数是39
- B.中位数与众数一定相等
- C.平均数可能为39
- D.平均数
 满足39<
满足39< <40
<40
D
分析:根据平均数、众数、中位数的概念分析各个选项,即可得出答案.
解答:A、由于38、41、42码的数和为10,而39、40码对应的数不知,故不能确定出中位数和众数,故错误;
B、由于38、41、42码的数和为10,而39、40码对应的数不知,故不能确定出中位数和众数,也就不能确定出中位数与众数是否相等,故错误;
C、当39码的数为10,40码的数为0时,平均数=(38×5+39×10+41×3+42×2)÷20=39.35;
当39码的数为0,40码的数为10时,平均数=(38×5+40×10+41×3+42×2)÷20=39.85;
∴这组数据的平均数 满足39<
满足39< <40,
<40,
所以平均数不可能是39,故本选项错误;
D、当39码的数为10,40码的数为0时,平均数=(38×5+39×10+41×3+42×2)÷20=39.35;
当39码的数为0,40码的数为10时,平均数=(38×5+40×10+41×3+42×2)÷20=39.85;
∴这组数据的平均数 满足39<
满足39< <40,故本选项正确;
<40,故本选项正确;
故选D.
点评:平均数是指在一组数据中所有数据之和再除以数据的个数.众数是数据中出现次数最多的数,中位数是数据从小到大排列后,最中间的数(或中间两数的平均数)是中位数.
分析:根据平均数、众数、中位数的概念分析各个选项,即可得出答案.
解答:A、由于38、41、42码的数和为10,而39、40码对应的数不知,故不能确定出中位数和众数,故错误;
B、由于38、41、42码的数和为10,而39、40码对应的数不知,故不能确定出中位数和众数,也就不能确定出中位数与众数是否相等,故错误;
C、当39码的数为10,40码的数为0时,平均数=(38×5+39×10+41×3+42×2)÷20=39.35;
当39码的数为0,40码的数为10时,平均数=(38×5+40×10+41×3+42×2)÷20=39.85;
∴这组数据的平均数
 满足39<
满足39< <40,
<40,所以平均数不可能是39,故本选项错误;
D、当39码的数为10,40码的数为0时,平均数=(38×5+39×10+41×3+42×2)÷20=39.35;
当39码的数为0,40码的数为10时,平均数=(38×5+40×10+41×3+42×2)÷20=39.85;
∴这组数据的平均数
 满足39<
满足39< <40,故本选项正确;
<40,故本选项正确;故选D.
点评:平均数是指在一组数据中所有数据之和再除以数据的个数.众数是数据中出现次数最多的数,中位数是数据从小到大排列后,最中间的数(或中间两数的平均数)是中位数.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
(2012•太原二模)某校七年级运动队为了备战校运动会需要购置一批运动鞋.已知该队伍有20名同学,统计表如下表.由于不小心弄脏了表格,有两个数据看不到.
|
某校七年级运动队为了备战校运动会需要购置一批运动鞋.已知该队伍有20名同学,统计表如下表.由于不小心弄脏了表格,有两个数据看不到.
下列关于鞋码说法中正确的是( )
A.中位数是40,众数是39
B.中位数与众数一定相等
C.平均数可能为39
D.平均数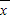 满足39<
满足39<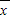 <40
<40
| 鞋码 | 38 | 39 | 40 | 41 | 42 |
| 人数 | 5 | 3 | 2 |
A.中位数是40,众数是39
B.中位数与众数一定相等
C.平均数可能为39
D.平均数
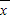 满足39<
满足39<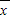 <40
<40