题目内容
学习了勾股定理以后,有同学提出“在直角三角形中,三边满足a2+b2=c2,或许其他的三角形三边也有这样的关系”.让我们来做一个实验!
(1)画出任意一个锐角三角形,量出各边的长度(精确到1毫米),较短的两条边长分别是a=______mm;b=______mm;较长的一条边长c=______mm.比较=a2+b2______c2(填写“>”,“<”,或“=”);
(2)画出任意的一个钝角三角形,量出各边的长度(精确到1毫米),较短的两条边长分别是a=______mm;b=______mm;较长的一条边长c=______mm.比较a2+b2______c2(填写“>”,“<”,或“=”);
(3)根据以上的操作和结果,对这位同学提出的问题,你猜想的结论是:______,类比勾股定理的验证方法,相信你能说明其能否成立的理由.
解:(1)较短的两条边长分别是a=6mm;b=8mm;较长的一条边长c=9mm.比较=a2+b2>c2;
(2)较短的两条边长分别是a=6mm;b=8mm;较长的一条边长c=11mm.比较a2+b2<c2;
(3)若△ABC是锐角三角形,则有a2+b2>c2;
若△ABC是钝角三角形,∠C为钝角,则有a2+b2<c2.
当△ABC是锐角三角形时,
理由:过点A作AD⊥BC,垂足为D,设CD为x,

则有BD=a-x.
根据勾股定理,得b2-x2=AD2=c2-(a-x)2,
即b2-x2=c2-a2+2ax-x2.
∴a2+b2=c2+2ax.
∵a>0,x>0,
∴2ax>0;
∴a2+b2>c2.
当△ABC是钝角三角形时,
理由:过C作CD⊥AB,交AB的延长线于D.
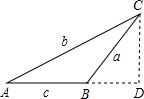
设BD为x,则有CD2=a2-x2,
根据勾股定理,得(c+x)2+a2-x2=b2,即a2+c2+2cx=b2.
∵c>0,x>0,
∴2cx>0,
∴a2+c2<b2.
分析:熟悉勾股数,然后根据大边对大角,小边对小角,确定第三边的长,从而保证三角形的形状.如取较小的两边是6,8,若是直角三角形,则第三边应是10.故要保证它是锐角三角形,只需取9.要保证它是钝角三角形,只需取11.
证明的时候,充分运用勾股定理结合完全平方公式即可分析证明.
点评:本题考查了勾股定理的证明,在给定三角形的三边的时候,还要注意三角形的三边关系.注意勾股定理的熟练运用以及完全平方公式的灵活变形.
(2)较短的两条边长分别是a=6mm;b=8mm;较长的一条边长c=11mm.比较a2+b2<c2;
(3)若△ABC是锐角三角形,则有a2+b2>c2;
若△ABC是钝角三角形,∠C为钝角,则有a2+b2<c2.
当△ABC是锐角三角形时,
理由:过点A作AD⊥BC,垂足为D,设CD为x,

则有BD=a-x.
根据勾股定理,得b2-x2=AD2=c2-(a-x)2,
即b2-x2=c2-a2+2ax-x2.
∴a2+b2=c2+2ax.
∵a>0,x>0,
∴2ax>0;
∴a2+b2>c2.
当△ABC是钝角三角形时,
理由:过C作CD⊥AB,交AB的延长线于D.

设BD为x,则有CD2=a2-x2,
根据勾股定理,得(c+x)2+a2-x2=b2,即a2+c2+2cx=b2.
∵c>0,x>0,
∴2cx>0,
∴a2+c2<b2.
分析:熟悉勾股数,然后根据大边对大角,小边对小角,确定第三边的长,从而保证三角形的形状.如取较小的两边是6,8,若是直角三角形,则第三边应是10.故要保证它是锐角三角形,只需取9.要保证它是钝角三角形,只需取11.
证明的时候,充分运用勾股定理结合完全平方公式即可分析证明.
点评:本题考查了勾股定理的证明,在给定三角形的三边的时候,还要注意三角形的三边关系.注意勾股定理的熟练运用以及完全平方公式的灵活变形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目