题目内容
在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG.
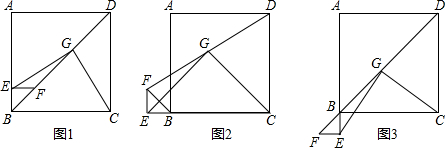
(1)如图1,则线段EG和CG有怎样的数量关系和位置关系?
(2)将△BEF绕点B逆时针旋转90°,如图2;将△BEF绕点B逆时针旋转180°,如图3,则(1)中的结论还成立吗?如果成立请选择三图中任一图加以证明;如果不成立,请说明理由.

(1)如图1,则线段EG和CG有怎样的数量关系和位置关系?
(2)将△BEF绕点B逆时针旋转90°,如图2;将△BEF绕点B逆时针旋转180°,如图3,则(1)中的结论还成立吗?如果成立请选择三图中任一图加以证明;如果不成立,请说明理由.
分析:(1)过点G作GH⊥BD于G交CD于H,通过条件证明△EFG≌△CHG,就可以得出结论EG=CG,EG⊥CG;
(2)作GH⊥BC于H,根据平行线等分线段定理就可以得出EH=CH,再根据中垂线的性质就可以得出EG=EC,过点G作GP⊥BD于G交CB于P,最后通过证明三角形全等就可以得出结论EG⊥CG;
(2)作GH⊥BC于H,根据平行线等分线段定理就可以得出EH=CH,再根据中垂线的性质就可以得出EG=EC,过点G作GP⊥BD于G交CB于P,最后通过证明三角形全等就可以得出结论EG⊥CG;
解答: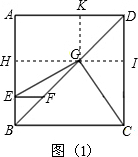 (1)EG=CG,且EG⊥CG.
(1)EG=CG,且EG⊥CG.
证明:过GH⊥AB于点H,延长HG交CD于点I,作GK⊥AD于点K.
则四边形GIDK是正方形,四边形AKGH是矩形,
∴AK=HG,KD=DI=GI=AH,
∵AD=CD,
∴IC=HG,
∵AD∥GH∥EF,G是DF的中点,
∴HA=HE,
∴HE=GI,
∵在Rt△HGE和Rt△ICG中,
,
∴Rt△HGE≌Rt△ICG(SAS),
∴EG=CG,∠HGE=∠GCI,∠HEG=∠CGI,
∴∠HGE+∠CGI=90°,
∴∠EGC=90°,
∴EG⊥CG;
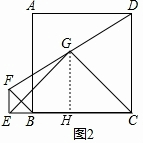
(2)成立.
证明:图2中,作GH⊥BC,
则EF∥GH∥CD,
又∵G是DF的中点,
∴EH=CH,
则GH是BC的中垂线,
∴GE=CG,
∵EF=EB,BC=CD
∴EF+CD=EC,
∵G是DF的中点,EH=CH,
则GH=
(EF+CD),
∴GH=
EC,
∴△EGC是等腰直角三角形,
∴EG=CG,且EG⊥CG;
图3中,延长FE交DC延长线于M,连MG.
∵∠AEM=90°,∠EBC=90°,∠BCM=90°,
∴四边形BEMC是矩形.
∴BE=CM,∠EMC=90°,
由图(2)可知,
∵BD平分∠ABC,∠ABC=90°,
∴∠EBF=45°,
又∵EF⊥AB,
∴△BEF为等腰直角三角形
∴BE=EF,∠F=45°.
∴EF=CM.
∵∠EMC=90°,FG=DG
∴MG=
FD=FG.
∵BC=EM,BC=CD,
∴EM=CD.
∵EF=CM,
∴EF+EM=CM+DC,
即FM=DM,
又∵FG=DG,
∠CMG=
∠EMC=45°,
∴∠F=∠GMC.
∵在△GFE和△GMC中,
,
∴△GFE≌△GMC(SAS).
∴EG=CG,∠FGE=∠MGC.
∵∠FMC=90°,MF=MD,FG=DG,
∴MG⊥FD,
∴∠FGE+∠EGM=90°,
∴∠MGC+∠EGM=90°,
即∠EGC=90°,
∴EG⊥CG.
 (1)EG=CG,且EG⊥CG.
(1)EG=CG,且EG⊥CG.证明:过GH⊥AB于点H,延长HG交CD于点I,作GK⊥AD于点K.
则四边形GIDK是正方形,四边形AKGH是矩形,
∴AK=HG,KD=DI=GI=AH,
∵AD=CD,
∴IC=HG,
∵AD∥GH∥EF,G是DF的中点,
∴HA=HE,
∴HE=GI,
∵在Rt△HGE和Rt△ICG中,
|
∴Rt△HGE≌Rt△ICG(SAS),
∴EG=CG,∠HGE=∠GCI,∠HEG=∠CGI,
∴∠HGE+∠CGI=90°,
∴∠EGC=90°,
∴EG⊥CG;

(2)成立.
证明:图2中,作GH⊥BC,
则EF∥GH∥CD,
又∵G是DF的中点,
∴EH=CH,
则GH是BC的中垂线,
∴GE=CG,
∵EF=EB,BC=CD
∴EF+CD=EC,
∵G是DF的中点,EH=CH,
则GH=
| 1 |
| 2 |
∴GH=
| 1 |
| 2 |
∴△EGC是等腰直角三角形,
∴EG=CG,且EG⊥CG;
图3中,延长FE交DC延长线于M,连MG.
∵∠AEM=90°,∠EBC=90°,∠BCM=90°,
∴四边形BEMC是矩形.
∴BE=CM,∠EMC=90°,
由图(2)可知,
∵BD平分∠ABC,∠ABC=90°,
∴∠EBF=45°,
又∵EF⊥AB,
∴△BEF为等腰直角三角形
∴BE=EF,∠F=45°.
∴EF=CM.
∵∠EMC=90°,FG=DG

∴MG=
| 1 |
| 2 |
∵BC=EM,BC=CD,
∴EM=CD.
∵EF=CM,
∴EF+EM=CM+DC,
即FM=DM,
又∵FG=DG,
∠CMG=
| 1 |
| 2 |
∴∠F=∠GMC.
∵在△GFE和△GMC中,
|
∴△GFE≌△GMC(SAS).
∴EG=CG,∠FGE=∠MGC.
∵∠FMC=90°,MF=MD,FG=DG,
∴MG⊥FD,
∴∠FGE+∠EGM=90°,
∴∠MGC+∠EGM=90°,
即∠EGC=90°,
∴EG⊥CG.
点评:此题综合考查了旋转的性质及全等三角形的判断和性质,如何构造全等的三角形是难点,因此难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

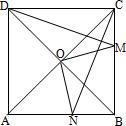 42、如图,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM交AB于N,设正方形对角线交点为O,试确定OM与ON之间的关系,并说明理由.
42、如图,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM交AB于N,设正方形对角线交点为O,试确定OM与ON之间的关系,并说明理由.

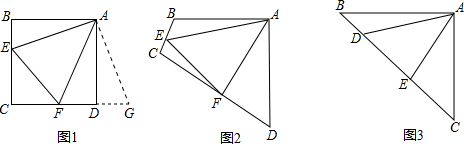
 如图,正方形CEFG的对角线CF在正方形ABCD的边BC的延长线上(CE>BC),点M在CF上,且MF=AB,线段AF与DM交于点N.
如图,正方形CEFG的对角线CF在正方形ABCD的边BC的延长线上(CE>BC),点M在CF上,且MF=AB,线段AF与DM交于点N.