题目内容
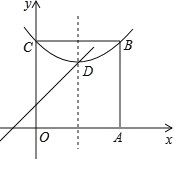
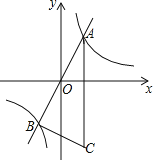
【题目】如图,反比例函数y=![]() (k≠0)的图象与正比例函数y=2x的图象相交于A(1,a)、B两点,点C在第四象限,CA∥y轴,且CB⊥AB.
(k≠0)的图象与正比例函数y=2x的图象相交于A(1,a)、B两点,点C在第四象限,CA∥y轴,且CB⊥AB.
(1)求反比例函数的解析式及点B的坐标;
(2)求tanC的值和△ABC的面积.
【答案】(1)![]() ,B(﹣1,﹣2);(2)tanC=2,S△ABC=5.
,B(﹣1,﹣2);(2)tanC=2,S△ABC=5.
【解析】
(1)先利用正比例函数解析式确定A(1,2),再把A点坐标代入y=![]() 中求出k得到反比例函数解析式为y=
中求出k得到反比例函数解析式为y=![]() ,然后根据中心对称求得B点坐标;
,然后根据中心对称求得B点坐标;
(2)作BD⊥AC于D,如图,利用等角的余角相等得到∠C=∠ABD,然后在在Rt△ABD中利用正切的定义即可求得tanC的值,根据勾股定理求得AB,通过证明△ADO~△ABC,根据相似三角形的性质即可求得△ABC的面积.
解:(1)∵点A(1,a)在y=2x上,
∴a=2,
∴A(1,2),
把A(1,2)代入![]() 得k=2
得k=2
∴反比例函数的解析式为![]() ,
,
∵A、B两点关于原点成中心对称,
∴B(﹣1,﹣2);
(2)如图所示,作BH⊥AC于H,设AC交x轴于点D,
∵∠ABC=90°,∠BHC=90°,
∴∠C=∠ABH,
∵BH∥x轴
∴∠AOD=∠ABH,
∴∠AOD=∠C,
∴![]() ,
,
∵A(1,2),B(﹣1,﹣2),
∴AH=4,BH=2,OD=1,AD=2,
∴![]() ,S△AOD=
,S△AOD=![]() =1,
=1,
∵∠AOD=∠C,∠ADO=∠ABC=90°,
∴△ADO~△ABC,
∴有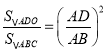 ,即
,即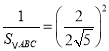 ,
,
解得S△ABC=5.


练习册系列答案
相关题目