题目内容
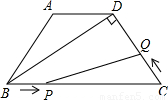
(2003•青岛)巳知:如图,梯形ABCD中,AD∥BC,AB=CD=3cm,∠C=60°,BD⊥CD.(1)求BC、AD的长度;
(2)若点P从点B开始沿BC边向点C以2cm/秒的速度运动,点Q从点C开始沿CD边向点D以1cm/秒的速度运动,当P、Q分别从B、C同时出发时,写出五边形ABPQD的面积S与运动时间t之间的函数关系式,并写出自变量t的取值范围(不包含点P在B、C两点的情况);
(3)在(2)的前提下,是否存在某一时刻t,使线段PQ把梯形ABCD分成两部分的面积比为1:5?若存在,求出t的值;若不存在,请说明理由.
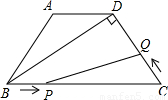
【答案】分析:(1)在Rt△BCD中,CD=3cm,∠C=60°根据三角函数就可以求出BC的长.∠ABD=∠ABC-∠DBC=30°,即∠ABD=∠ADB根据等角对等边,就可以得到AD=AB.
(2)写出五边形ABPQD的面积S是梯形ABCD的面积与△PCQ的面积的差,梯形ABCD的面积容易得到.△PCQ中PC容易用时间t表示出来,PC边上的高,根据三角形相似就可以表示出来,从而五边形ABPQD的面积S与运动时间t之间的函数关系式就可以求出来.
(3)线段PQ把梯形ABCD分成两部分的面积比为1:5,即五边形ABPQD的面积S是梯形面积的 或
或 ,就可以得到方程,解方程,就可以求出t的值.
,就可以得到方程,解方程,就可以求出t的值.
解答:解:(1)在Rt△BCD中,CD=3cm,∠C=60°
∴∠DBC=30°
∴BC=2CD=6cm
由已知得:梯形ABCD是等腰梯形
∴∠ABC=∠C=60°
∴∠ABD=∠ABC-∠DBC=30°
∵AD∥BC,
∴∠ADB=∠DBC=30°
∴∠ABD=∠ADB
∴AD=AB=3cm
(2)当P、Q分别从B、C同时出发运动t秒时,BP=2t,CQ=t
∴PC=6-2t
过Q作QE⊥BC于E,则QE=CQsin60°=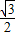 t
t
∴S梯形ABCD-S△PCQ=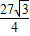 -
-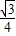 (6-2t)t=
(6-2t)t=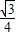 (2t2-6t+27)(0<t<3)
(2t2-6t+27)(0<t<3)
(3)存在时刻t,使线段PQ把梯形ABCD分成两部分的面积比为1:5
∵S梯形ABCD= ,S△ABD=
,S△ABD= ×3×
×3× ×3
×3
∴S△ABD= ×S梯形ABCD
×S梯形ABCD
∴五边形ABPQD的面积不可能是梯形ABCD面积的
∴S△PCQ:S五边形ABPQD=1:5,
即S五边形ABPQD= S梯形ABCD
S梯形ABCD
∴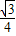 (2t2-6t+27)=
(2t2-6t+27)= ×
×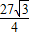
整理得:4t2-12t+9=0
∴t= ,即当t=
,即当t= 秒时,PQ把梯形ABCD分成两部分的面积比为1:5.
秒时,PQ把梯形ABCD分成两部分的面积比为1:5.
点评:本题是函数与梯形相结合的题目,注意数与形的结合是解题的关键.
(2)写出五边形ABPQD的面积S是梯形ABCD的面积与△PCQ的面积的差,梯形ABCD的面积容易得到.△PCQ中PC容易用时间t表示出来,PC边上的高,根据三角形相似就可以表示出来,从而五边形ABPQD的面积S与运动时间t之间的函数关系式就可以求出来.
(3)线段PQ把梯形ABCD分成两部分的面积比为1:5,即五边形ABPQD的面积S是梯形面积的
 或
或 ,就可以得到方程,解方程,就可以求出t的值.
,就可以得到方程,解方程,就可以求出t的值.解答:解:(1)在Rt△BCD中,CD=3cm,∠C=60°
∴∠DBC=30°
∴BC=2CD=6cm
由已知得:梯形ABCD是等腰梯形
∴∠ABC=∠C=60°
∴∠ABD=∠ABC-∠DBC=30°
∵AD∥BC,
∴∠ADB=∠DBC=30°
∴∠ABD=∠ADB
∴AD=AB=3cm
(2)当P、Q分别从B、C同时出发运动t秒时,BP=2t,CQ=t

∴PC=6-2t
过Q作QE⊥BC于E,则QE=CQsin60°=
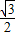 t
t∴S梯形ABCD-S△PCQ=
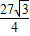 -
-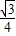 (6-2t)t=
(6-2t)t=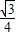 (2t2-6t+27)(0<t<3)
(2t2-6t+27)(0<t<3)(3)存在时刻t,使线段PQ把梯形ABCD分成两部分的面积比为1:5
∵S梯形ABCD=
 ,S△ABD=
,S△ABD= ×3×
×3× ×3
×3∴S△ABD=
 ×S梯形ABCD
×S梯形ABCD∴五边形ABPQD的面积不可能是梯形ABCD面积的

∴S△PCQ:S五边形ABPQD=1:5,
即S五边形ABPQD=
 S梯形ABCD
S梯形ABCD∴
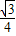 (2t2-6t+27)=
(2t2-6t+27)= ×
×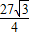
整理得:4t2-12t+9=0
∴t=
 ,即当t=
,即当t= 秒时,PQ把梯形ABCD分成两部分的面积比为1:5.
秒时,PQ把梯形ABCD分成两部分的面积比为1:5.点评:本题是函数与梯形相结合的题目,注意数与形的结合是解题的关键.

练习册系列答案
相关题目