题目内容
 如图∠AOB=180°,∠FOD=∠COE=90°
如图∠AOB=180°,∠FOD=∠COE=90°
(1)请写出∠EOF与∠COD的数量关系,并说明理由;
(2)写出∠AOF补角和余角;
(3)如果∠AOF=34°,OC平分∠BOD,求∠COB度数.
解:(1)∠EOF与∠COD的数量关系为相等.理由如下:
∵∠FOD=∠COE=90°,
∴∠EOF+∠DOE=∠DOE+∠COD,
∴∠EOF=∠COD;
(2)∵∠AOB=180°,∠FOD=∠COE=90°,
∴∠AOF补角为∠BOF,余角为∠BOD;
(3)∵∠AOF=34°,
∴∠BOD=90°-34°=56°,
∵OC平分∠BOD,
∴∠COB= ×56°=28°.
×56°=28°.
分析:(1)根据等角的余角相等可判断∠EOF=∠COD;
(2)根据补角与余角的定义求解;
(3)利用(2)中的结论得到∠BOD=90°-34°=56°,然后利用角平分线的定义求解.
点评:本题考查余角与补角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角;如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.
∵∠FOD=∠COE=90°,
∴∠EOF+∠DOE=∠DOE+∠COD,
∴∠EOF=∠COD;
(2)∵∠AOB=180°,∠FOD=∠COE=90°,
∴∠AOF补角为∠BOF,余角为∠BOD;
(3)∵∠AOF=34°,
∴∠BOD=90°-34°=56°,
∵OC平分∠BOD,
∴∠COB=
 ×56°=28°.
×56°=28°.分析:(1)根据等角的余角相等可判断∠EOF=∠COD;
(2)根据补角与余角的定义求解;
(3)利用(2)中的结论得到∠BOD=90°-34°=56°,然后利用角平分线的定义求解.
点评:本题考查余角与补角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角;如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.

练习册系列答案
相关题目
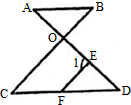 22、已知:如图,AB∥CD,EF∥BC,∠AOB=70°;∠1+∠C=150°,求∠B的度数.
22、已知:如图,AB∥CD,EF∥BC,∠AOB=70°;∠1+∠C=150°,求∠B的度数.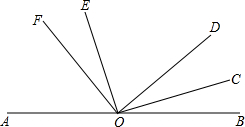 如图∠AOB=180°,∠FOD=∠COE=90°
如图∠AOB=180°,∠FOD=∠COE=90°