题目内容
如图,已知点A点C是一次函数y=x的图象与反比例函数y= 的图象的两个交点,点B在x轴的负
的图象的两个交点,点B在x轴的负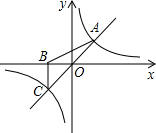 半轴上,且OA=OB,
半轴上,且OA=OB,
(1)求点A和点C的坐标;
(2)求△ACB的面积;
(3)直接写出不等式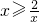 的解集.
的解集.
解:(1)解方程组 ,得
,得 或
或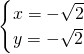 ,
,
∴A点坐标为( ,
, ),C点坐标为(-
),C点坐标为(- ,-
,- );
);
(2)∵A点坐标为( ,
, ),
),
∴OA= •
• =2,
=2,
∴OB=2,
∴S△ABC=S△AOB+S△OCB
= •2•
•2• +
+ •2•
•2• =2
=2 ;
;
(3)- <x<0或x>
<x<0或x> .
.
分析:(1)解方程组 即可得到点A和点C的坐标;
即可得到点A和点C的坐标;
(2)先计算出OA的长,得到OB的长,然后利用S△ABC=S△AOB+S△OCB和三角形的面积公式进行计算即可;
(3)看图可得到- <x<0或x>
<x<0或x> .
.
点评:本题考查了反比例函数和一次函数的交点问题:交点的横纵坐标满足两个函数图象的解析式,分别代入得到两个方程,解方程组即可确定交点坐标.也考查了观察函数图象的能力以及三角形的面积公式.
 ,得
,得 或
或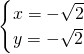 ,
,∴A点坐标为(
 ,
, ),C点坐标为(-
),C点坐标为(- ,-
,- );
);(2)∵A点坐标为(
 ,
, ),
),∴OA=
 •
• =2,
=2,∴OB=2,
∴S△ABC=S△AOB+S△OCB
=
 •2•
•2• +
+ •2•
•2• =2
=2 ;
;(3)-
 <x<0或x>
<x<0或x> .
.分析:(1)解方程组
 即可得到点A和点C的坐标;
即可得到点A和点C的坐标;(2)先计算出OA的长,得到OB的长,然后利用S△ABC=S△AOB+S△OCB和三角形的面积公式进行计算即可;
(3)看图可得到-
 <x<0或x>
<x<0或x> .
.点评:本题考查了反比例函数和一次函数的交点问题:交点的横纵坐标满足两个函数图象的解析式,分别代入得到两个方程,解方程组即可确定交点坐标.也考查了观察函数图象的能力以及三角形的面积公式.

练习册系列答案
相关题目
 第一象内的点过点P作PM⊥x轴于M、PN⊥y轴于N.两垂线与直线AB交于E、F.
第一象内的点过点P作PM⊥x轴于M、PN⊥y轴于N.两垂线与直线AB交于E、F.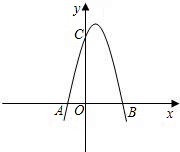 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8). 半轴上,且OA=OB,
半轴上,且OA=OB,
 (x>0)上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点,若△ABP的面积为3,则k=______。
(x>0)上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点,若△ABP的面积为3,则k=______。