题目内容
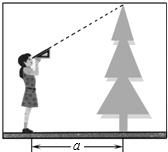 小莉站在离一棵树水平距离为a米的地方,用一块含30°的直角三角板按如图所示的方式测量这棵树的高度,已知小莉的眼睛离地面的高度是1.5米,那么她测得这棵树的高度为( )
小莉站在离一棵树水平距离为a米的地方,用一块含30°的直角三角板按如图所示的方式测量这棵树的高度,已知小莉的眼睛离地面的高度是1.5米,那么她测得这棵树的高度为( )A、(
| ||||
B、(
| ||||
C、(1.5+
| ||||
D、(1.5+
|
分析:过小莉的视点作树的垂线,通过构建直角三角形来求这棵树的高度.
解答: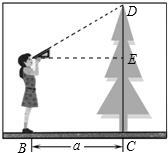 解:如图.过A作CD的垂线,设垂足为E点,
解:如图.过A作CD的垂线,设垂足为E点,
则AE=BC=a,AB=CE=1.5米.
Rt△ADE中,AE=a,∠DAE=30°,
∴DE=AE•tan30°=
a(米),
∴CD=CE+DE=(
a+1.5)米.
故选C.
 解:如图.过A作CD的垂线,设垂足为E点,
解:如图.过A作CD的垂线,设垂足为E点,则AE=BC=a,AB=CE=1.5米.
Rt△ADE中,AE=a,∠DAE=30°,
∴DE=AE•tan30°=
| ||
| 3 |
∴CD=CE+DE=(
| ||
| 3 |
故选C.
点评:此题考查了仰角的定义及通过解直角三角形解决实际问题的能力.构造直角三角形是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 米 B.
米 B. 米
米  米 D.
米 D. 米
米
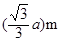 B.
B.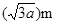
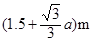 D.
D.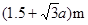

 )米
)米 a)米
a)米 )米
)米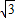 a)米
a)米
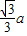 )米
)米 a)米
a)米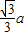 )米
)米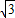 a)米
a)米