题目内容
【题目】如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y= ![]() (x<0)的图象经过点A,若S△ABO=
(x<0)的图象经过点A,若S△ABO= ![]() ,则k的值为 .
,则k的值为 . 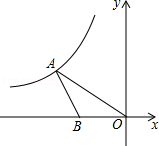
【答案】﹣3 ![]()
【解析】解:过点A作AD⊥x轴于点D,如图所示. 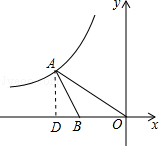
∵∠AOB=30°,AD⊥OD,
∴ ![]() =cot∠AOB=
=cot∠AOB= ![]() ,
,
∵∠AOB=30°,AB=BO,
∴∠AOB=∠BAO=30°,
∴∠ABD=60°,
∴ ![]() =cot∠ABD=
=cot∠ABD= ![]() ,
,
∵OB=OD﹣BD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵S△ABO= ![]() ,
,
∴S△ADO= ![]() |k|=
|k|= ![]() ,
,
∵反比例函数图象在第二象限,
∴k=﹣3 ![]()
故答案为:﹣3 ![]() .
.
过点A作AD⊥x轴于点D,由∠AOB=30°可得出 ![]() =
= ![]() ,再根据BA=BO可得出∠ABD=60°,由此可得出
,再根据BA=BO可得出∠ABD=60°,由此可得出 ![]() =
= ![]() ,根据线段间的关系即可得出线段OB、OD间的比例,结合反比例函数系数k的几何意义以及S△ABO=
,根据线段间的关系即可得出线段OB、OD间的比例,结合反比例函数系数k的几何意义以及S△ABO= ![]() 即可得出结论.
即可得出结论.

练习册系列答案
相关题目
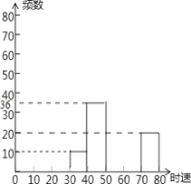
【题目】某路段某时段用雷达测速仪随机监测了200辆汽车的时速,得到如下频数分布表(不完整):注:30﹣40为时速大于或等于30千米而小于40千米,其它类同.
数据段 | 频数 |
30~40 | 10 |
_______ | 36 |
50~60 | 80 |
60~70 | _____ |
70~80 | 20 |
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此路段该时间段经过的车有1000辆.估计约有多少辆车的时速大于或等于 60千米.