题目内容
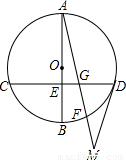
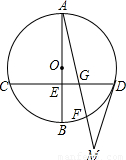
(2003•仙桃)如图,AB是⊙O的直径,弦CD⊥AB于E,弦CD、AF相交于点G,过点D作⊙O的切线交AF的延长线于M,且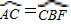 .
.(1)在图中找出相等的线段(直接在横线上填写,所写结论至少3组,所添辅助线段除外,不需写推理过程)______;
(2)连接AD,DF(请将图形补充完整),若AO=
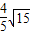 ,OE=
,OE=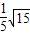 ,求AD:DF的值;
,求AD:DF的值;(3)在满足(1)、(2)的前提下,求DM的长.
【答案】分析:(1)本题中相等的弦较多,不一一列举,得出相等线段的方法大致有3种:
①⊙O的半径相等,如:OA=OB;②垂径定理,如:CE=DE;③等弧对等弦,如:AF=CD;
(2)已知OA、OE的长,即可得出AE、BE的值;根据相交弦定理的推论,可得DE2=AE•EB,由此可求出DE的长,也就求出了CD、DF的长,进而可在Rt△ADE中,求出AD的长,过证△ADG∽△AFD,得:AD2=AG•AF,可求出AG、GF的长,连接AC,易知:△ACG∽△FDG,得AC:DF=AG:GF,AG、GF的长已知,由此可求出AC、DF的比例关系,由于AC=AD,也就得出了AD:DF的值;
(3)先由△DMF∽△AMD,得出DM、AM的比例关系,然后用未知数表示出DM、AM、MF的长,进而可根据切割线定理求出DM的值.
解答: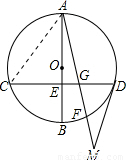 解:(1)CE=DE,OA=OB,CD=AF;
解:(1)CE=DE,OA=OB,CD=AF;
(2)由题意,知:AE=AO+OE=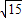 ,BE=OB-OE=
,BE=OB-OE=
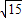 ,
,
由相交弦定理,知:DE2=AE•EB=9,即DE=3,CD=6,
Rt△ADE中,由勾股定理,得:
AD2=AE2+DE2=24
∵
∴∠ADG=∠AFD
∴△ADG∽△AFD
∴AD2=AG•AF,即AG=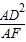 =4
=4
∴GF=AF-AG=2
连接AC,易证得△ACG∽△FDG
∴ =2
=2
∵
∴AD=AC,即 =2;
=2;
(3)∵MD切⊙O于D,
∴∠MDF=∠MAD
又∵∠FMD=∠DMA
∴△DMF∽△AMD
∴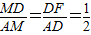
设MD=x,则AM=2x,MF=2x-6
由切割线定理,得:DM2=MF•AM
即:x2=(2x-6)×2x,解得x=4
即MD=4.
点评:本题主要考查了切线的性质,弦切角定理,切割线定理,垂径定理,弧、弦的关系以及相似三角形的判定和性质;涉及的知识点多,综合性强,难度较大.
①⊙O的半径相等,如:OA=OB;②垂径定理,如:CE=DE;③等弧对等弦,如:AF=CD;
(2)已知OA、OE的长,即可得出AE、BE的值;根据相交弦定理的推论,可得DE2=AE•EB,由此可求出DE的长,也就求出了CD、DF的长,进而可在Rt△ADE中,求出AD的长,过证△ADG∽△AFD,得:AD2=AG•AF,可求出AG、GF的长,连接AC,易知:△ACG∽△FDG,得AC:DF=AG:GF,AG、GF的长已知,由此可求出AC、DF的比例关系,由于AC=AD,也就得出了AD:DF的值;
(3)先由△DMF∽△AMD,得出DM、AM的比例关系,然后用未知数表示出DM、AM、MF的长,进而可根据切割线定理求出DM的值.
解答:
 解:(1)CE=DE,OA=OB,CD=AF;
解:(1)CE=DE,OA=OB,CD=AF;(2)由题意,知:AE=AO+OE=
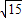 ,BE=OB-OE=
,BE=OB-OE=
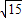 ,
,由相交弦定理,知:DE2=AE•EB=9,即DE=3,CD=6,
Rt△ADE中,由勾股定理,得:
AD2=AE2+DE2=24
∵

∴∠ADG=∠AFD
∴△ADG∽△AFD
∴AD2=AG•AF,即AG=
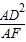 =4
=4∴GF=AF-AG=2
连接AC,易证得△ACG∽△FDG
∴
 =2
=2∵

∴AD=AC,即
 =2;
=2;(3)∵MD切⊙O于D,
∴∠MDF=∠MAD
又∵∠FMD=∠DMA
∴△DMF∽△AMD
∴
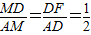
设MD=x,则AM=2x,MF=2x-6
由切割线定理,得:DM2=MF•AM
即:x2=(2x-6)×2x,解得x=4
即MD=4.
点评:本题主要考查了切线的性质,弦切角定理,切割线定理,垂径定理,弧、弦的关系以及相似三角形的判定和性质;涉及的知识点多,综合性强,难度较大.

练习册系列答案
相关题目
 .
.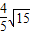 ,OE=
,OE=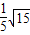 ,求AD:DF的值;
,求AD:DF的值;