题目内容
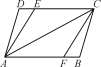
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 是
是 ![]() 的中点.将
的中点.将![]() 沿
沿 ![]() 对折至
对折至![]() , 延长
, 延长![]() 交
交 ![]() 于点
于点 ![]() ,则
,则![]() 的长是____.
的长是____.

【答案】4
【解析】
连接AE,由折叠的性质知,∠AFG=∠AFE=∠B=90°,AF=AB=AD.然后可证Rt△AEF≌Rt△AED,从而DE=DF,设DE=DF=x,则CE=12-x,GE=6+x.在Rt△CGE中,利用勾股定理列方程求解即可.
连接AE.
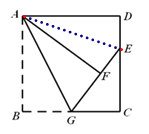
∵![]() 是
是 ![]() 的中点,
的中点,
∴GF=BG=12÷2=6.
由折叠的性质知,∠AFG=∠AFE=∠B=90°,AF=AB=AD.
在Rt△AEF和Rt△AED中
∵AF=AD,
AE=AE,
∴Rt△AEF≌Rt△AED,
∴DE=DF.
设DE=DF=x,则CE=12-x,GE=6+x.
∵CG2+CE2=GE2,
∴62+(12-x)2=(6+x)2,
解之得
x=4.
故答案为:4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.