题目内容
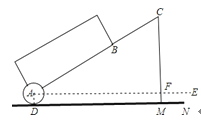
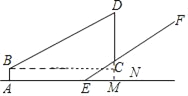
【题目】如图,在斜坡EF上有一信号发射塔CD,某兴趣小组想要测量发射塔CD的高度,于是在水平地面用仪器测得塔顶D的仰角为31°,已知仪器AB高为2m,斜坡EF的坡度为i=3:4,塔底距离坡底的距离CE=10m,最后测得塔高为12m,A、B、C、D、E在同一平面内,则仪器到坡底距离AE约为( )米(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)

A. 18.6 B. 18.7 C. 22.0 D. 24.0
【答案】B
【解析】
如图所示,延长DC交直线AE于点M,过点B作BN∥AM交DM于点N,可得Rt△CEM、Rt△BDC和矩形ABNM,利用坡度3:4及勾股定理求出CM、EM的长,结合矩形的性质可求出的DC的长,再利用正切即可得出答案.
解:延长DC交直线AE于点M,过点B作BN∥AM交DM于点N,
∵DM⊥AE,AB⊥AE,BN∥AM,
∴△CEM、△BDC是直角三角形,四边形ABNM是矩形,
∴BN=AM,MN=AB=2m,
在Rt△CEM中,由于CE=10m,i=3:4=CM:EM,
∴CM=![]() EM,
EM,
∵CE2=CM2+EM2,
∴EM=8m,CM=6m,
∴CN=CM﹣MN=4m,DN=DC+CN=12+4=16(m),
在Rt△CDB中,
∵tan∠DBN=![]() ,
,
∴AM=BN=![]() =
=![]() ≈
≈![]() ≈26.67(m),
≈26.67(m),
∴AE=AM﹣EM=26.67﹣8≈18.7(m).
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目