题目内容
如图,△AOB是边长为2的等边三角形,过点A的直线y=- x+m与x轴交于点E.
x+m与x轴交于点E.(1)求点E的坐标;
(2)求过A、O、E三点的抛物线的解析式.

【答案】分析:(1)把A点的坐标代入过点A的直线解析式,求出直线方程,E点纵坐标为0,代入可求解点E的坐标.
(2)求抛物线的解析式,因为过原点O及点E,所以常数项为0,进而求出其抛物线即可.
解答:解:(1)易求得A为(1,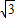 )把A(1,
)把A(1,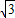 )代入y=-
)代入y=-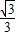 x+m得:
x+m得:
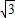 =-
=-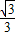 +m
+m
∴m=
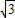
∴y=-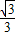 x+
x+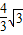
令y=0得,x=4,
∴E为(4,0);
(2)因为抛物线过原点及x轴上的点E,
∴常数项为0,又点E的坐标为(4,0)
可设y=ax(x-4)
又抛物线过点A(1, ),
),
所以可得y=-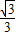 x2+
x2+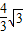 x.
x.
即y=-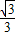 x(x-4).
x(x-4).
点评:熟练掌握等边三角形的性质,会用待定系数法求二次函数的解析式.
(2)求抛物线的解析式,因为过原点O及点E,所以常数项为0,进而求出其抛物线即可.
解答:解:(1)易求得A为(1,
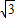 )把A(1,
)把A(1,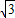 )代入y=-
)代入y=-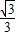 x+m得:
x+m得: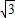 =-
=-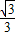 +m
+m∴m=

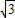
∴y=-
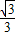 x+
x+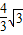
令y=0得,x=4,
∴E为(4,0);
(2)因为抛物线过原点及x轴上的点E,
∴常数项为0,又点E的坐标为(4,0)
可设y=ax(x-4)
又抛物线过点A(1,
 ),
),所以可得y=-
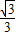 x2+
x2+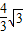 x.
x.即y=-
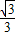 x(x-4).
x(x-4).点评:熟练掌握等边三角形的性质,会用待定系数法求二次函数的解析式.

练习册系列答案
相关题目
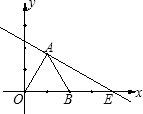 如图,△AOB是边长为2的等边三角形,过点A的直线y=-
如图,△AOB是边长为2的等边三角形,过点A的直线y=-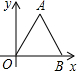 如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A
如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A x+m与x轴交于点E.
x+m与x轴交于点E.
 x+m与x轴交于点E.
x+m与x轴交于点E.