题目内容
等腰三角形底边长10 cm,腰长为13,则此三角形的面积为
- A.40
- B.50
- C.60
- D.70
C
试题分析:先作出图形,再根据勾股定理得出三角形的高,即可得到面积.
如图,等边△ABC中,BC=10cm,AB=AC=13cm,作AD⊥BC,垂足为D,
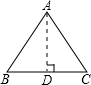
则D为BC中点,BD=CD=5cm,
在Rt△ABD中,
AD2=AB2-BD2=132-52=144,
∴AD=12cm,
∴S△ABC=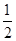 ×10×12=60(cm2).
×10×12=60(cm2).
故选C.
考点:本题考查的是勾股定理,等腰三角形的性质
点评:解答本题的关键是熟练掌握等腰三角形的“三线合一”的性质。
试题分析:先作出图形,再根据勾股定理得出三角形的高,即可得到面积.
如图,等边△ABC中,BC=10cm,AB=AC=13cm,作AD⊥BC,垂足为D,

则D为BC中点,BD=CD=5cm,
在Rt△ABD中,
AD2=AB2-BD2=132-52=144,
∴AD=12cm,
∴S△ABC=
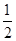 ×10×12=60(cm2).
×10×12=60(cm2).故选C.
考点:本题考查的是勾股定理,等腰三角形的性质
点评:解答本题的关键是熟练掌握等腰三角形的“三线合一”的性质。

练习册系列答案
相关题目