题目内容
 如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接AC,将矩形纸片OABC沿AC折叠,使点B落在点D的位置,若B(1,2),则点D的横坐标是( )
如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接AC,将矩形纸片OABC沿AC折叠,使点B落在点D的位置,若B(1,2),则点D的横坐标是( )分析:首先过点D作DF⊥OA于F,由四边形OABC是矩形与折叠的性质,易证得△AEC是等腰三角形,然后在Rt△AEO中,利用勾股定理求得AE,OE的长,然后由平行线分线段成比例定理求得AF的长,即可得点D的横坐标.
解答:解:过点D作DF⊥OA于F,
∵四边形OABC是矩形,
∴OC∥AB,
∴∠ECA=∠CAB,
根据题意得:∠CAB=∠CAD,∠CDA=∠B=90°,
∴∠ECA=∠EAC,
∴EC=EA,
∵B(1,2),
∴AD=AB=2,
设OE=x,则AE=EC=OC-OE=2-x,
在Rt△AOE中,AE2=OE2+OA2,
即(2-x)2=x2+1,
解得:x=
,
∴OE=
,AE=
,
∵DF⊥OA,OE⊥OA,
∴OE∥DF,
∴
=
=
=
=
,
∴AF=
,
∴OF=AF-OA=
,
∴点D的横坐标为:-
.
故选:D.
∵四边形OABC是矩形,
∴OC∥AB,
∴∠ECA=∠CAB,
根据题意得:∠CAB=∠CAD,∠CDA=∠B=90°,
∴∠ECA=∠EAC,
∴EC=EA,
∵B(1,2),
∴AD=AB=2,
设OE=x,则AE=EC=OC-OE=2-x,
在Rt△AOE中,AE2=OE2+OA2,
即(2-x)2=x2+1,

解得:x=
| 3 |
| 4 |
∴OE=
| 3 |
| 4 |
| 5 |
| 4 |
∵DF⊥OA,OE⊥OA,
∴OE∥DF,
∴
| AO |
| AF |
| OE |
| FD |
| AE |
| AD |
| ||
| 2 |
| 5 |
| 8 |
∴AF=
| 8 |
| 5 |
∴OF=AF-OA=
| 3 |
| 5 |
∴点D的横坐标为:-
| 3 |
| 5 |
故选:D.
点评:此题考查了折叠的性质,矩形的性质,等腰三角形的判定与性质以及平行线分线段成比例定理等知识.此题综合性较强,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
相关题目
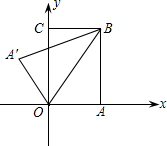 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB=
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB= ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 
 ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 

 ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 