题目内容
某工程机械厂根据市场需求,计划生产A、B两种型号的大型运输机械共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产此两种型号的大型运输机械,所生产的此两型大型运输机械可全部售出,此两型大型运输机械生产成本和售价如下表:
小题1:该厂对这两型大型运输机械有哪几种生产方案?
小题2:该厂如何生产能获得最大利润?
小题3:根据市场调查,每台B型大型运输机械的售价不会改变,每台A型大型运输机械的售价将会提高m万元(m>0),该厂应该如何生产可以获得最大利润?(注:利润=售价-成本)
| 型号 | A | B |
| 成本(万元/台) | 200 | 240 |
| 售价(万元/台) | 250 | 300 |
小题2:该厂如何生产能获得最大利润?
小题3:根据市场调查,每台B型大型运输机械的售价不会改变,每台A型大型运输机械的售价将会提高m万元(m>0),该厂应该如何生产可以获得最大利润?(注:利润=售价-成本)
小题1:见解析
小题1:见解析
小题1:见解析
小题1:解:设生产A型x台,则B型(100-x)台,由题意得
22400≤200x+240(100-x)≤22500,
解得37.5≤x≤40.
∵x取非负整数,∴x为38,39,40.
∴有三种生产方案:A型38台,B型62台;
A型39台,B型61台;
A型40台,B型60台
小题1:设获得利润W(万元),由题意得W=50x+60(100-x)=6000-10x
∴当x=38时,W最大=5620(万元),即生产A型38台,B型62台时,获得最大利润.
小题1:由题意得W=(50+m)x+60(100-x)=6000+(m-10)x
∴当0<m<10,则x=38时,W最大,即生产A型38台,B型62台;
当m=10时,m-10=0,则三种生产方案获得利润相等;
∴当m>10,则x=40时,W最大,
即生产A型40台,B型60台

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
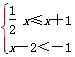 并写出它的所有整数解.
并写出它的所有整数解.
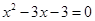
 的解集在数轴上表示为
的解集在数轴上表示为




