题目内容
 如图,点D在AB的中点,AC、DE分别垂直于BC,AB=7.4m,∠B=30°,则DE=( )
如图,点D在AB的中点,AC、DE分别垂直于BC,AB=7.4m,∠B=30°,则DE=( )| A、7.4m | B、3.7m | C、1.85m | D、14.8m |
分析:根据含30°的直角三角形的性质求出AC长,根据DE∥AC和点D在AB的中点,推出点E在BC的中点,得出DE=
AC,代入求出即可.
| 1 |
| 2 |
解答:解:∵AC⊥BC,
∴∠ACB=90°,
∵∠B=30°,
∴AC=
AB=
×7.4m=3.7m,
∵DE⊥BC,AC⊥BC,
∴DE∥AC,
∵点D在AB的中点,
∴点E在BC的中点,
∴DE=
AC=
×3.7m=1.85m.
故选C.
∴∠ACB=90°,
∵∠B=30°,
∴AC=
| 1 |
| 2 |
| 1 |
| 2 |
∵DE⊥BC,AC⊥BC,
∴DE∥AC,
∵点D在AB的中点,
∴点E在BC的中点,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题主要考查对三角形的中位线定理,含30度角的直角三角形的性质,平行线分线段成比例定理等知识点的理解和掌握,能求出AC的长和推出DE=
AC是解此题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
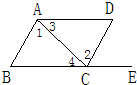 1、如图,点E在AC的延长线上,下列条件中能判断AB∥CD( )
1、如图,点E在AC的延长线上,下列条件中能判断AB∥CD( )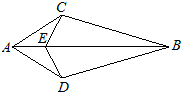 21、如图,点E在AB上,AC=AD,∠CAB=∠DAB.请你写出图中两对全等三角形,并就其中的一对给予证明.
21、如图,点E在AB上,AC=AD,∠CAB=∠DAB.请你写出图中两对全等三角形,并就其中的一对给予证明. 19、如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.所添条件为
19、如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.所添条件为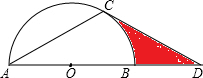 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠A=30°.
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠A=30°. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧交AB于M、AC于N,再分别以M、N为圆心,大于
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧交AB于M、AC于N,再分别以M、N为圆心,大于