题目内容
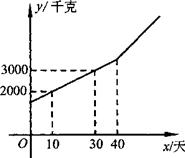
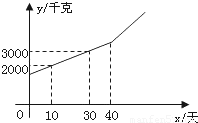
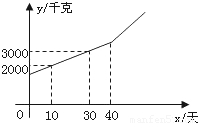
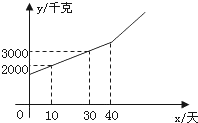 某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.(1)分别求出x≤40和x≥40时y与x之间的关系式;
(2)如果这些农作物每天的需水量大于或等于4000千克时需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
分析:(1)设y=kx+b.把已知坐标代入求出k,b的值.求出y与x的函数关系式;
再根据x的取值求出各段的函数解析式;
(2)令y≥4000时,转化为不等式问题求解.
再根据x的取值求出各段的函数解析式;
(2)令y≥4000时,转化为不等式问题求解.
解答:解:(1)当x≤40时,设y=kx+b.
根据题意,得
解这个方程组,得
∴当x≤40时,y与x之间的关系式是y=50x+1500;(4分)
∴当x=40时,y=50×40+1500=3500;
当x≥40时,根据题意,得y=100(x-40)+3500,即y=100x-500.
∴当x≥40时,y与x之间的关系式是y=100x-500.(6分)
(2)当y≥4000时,y与x之间的关系式是y=100x-500.
解不等式100x-500≥4000.
得x≥45.
∴应从第45天开始进行人工灌溉.(8分)
根据题意,得
|
解这个方程组,得
|
∴当x≤40时,y与x之间的关系式是y=50x+1500;(4分)
∴当x=40时,y=50×40+1500=3500;
当x≥40时,根据题意,得y=100(x-40)+3500,即y=100x-500.
∴当x≥40时,y与x之间的关系式是y=100x-500.(6分)
(2)当y≥4000时,y与x之间的关系式是y=100x-500.
解不等式100x-500≥4000.
得x≥45.
∴应从第45天开始进行人工灌溉.(8分)
点评:本题通过一次函数的知识,考查学生解决实际问题的能力,要求学生根据问题提供的信息读懂图象,并善于从图象中得到正确的信息.要求学生将所给的函数图象与其表示的实际意义联系起来,并结合图象分析和解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (千克)与生长时间
(千克)与生长时间 (天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.