题目内容
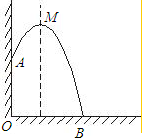
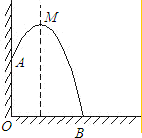 某幢建筑物,从10m高的窗口A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图,如果抛物线的最高点M离墙1m,离地面
某幢建筑物,从10m高的窗口A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图,如果抛物线的最高点M离墙1m,离地面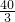 m,则水流落地点B离墙的距离OB是
m,则水流落地点B离墙的距离OB是
- A.2m
- B.3m
- C.4m
- D.5m
B
分析:以OB为x轴,OA为y轴建立平面直角坐标系,A点坐标为(0,10),M点的坐标为(1,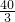 ),设出抛物线的解析式,代入解答球的函数解析式,进一步求得问题的解.
),设出抛物线的解析式,代入解答球的函数解析式,进一步求得问题的解.
解答:设抛物线的解析式为y=a(x-1)2+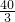 ,
,
把点A(0,10)代入a(x-1)2+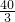 ,得a(0-1)2+
,得a(0-1)2+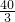 =10,
=10,
解得a=- ,
,
因此抛物线解析式为y=- (x-1)2+
(x-1)2+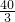 ,
,
当y=0时,解得x1=3,x2=-1(不合题意,舍去);
即OB=3米.
故选B.
点评:解答此题的关键是正确建立坐标系,求得函数解析式,再据具体条件利用解析式解决问题.
分析:以OB为x轴,OA为y轴建立平面直角坐标系,A点坐标为(0,10),M点的坐标为(1,
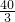 ),设出抛物线的解析式,代入解答球的函数解析式,进一步求得问题的解.
),设出抛物线的解析式,代入解答球的函数解析式,进一步求得问题的解.解答:设抛物线的解析式为y=a(x-1)2+
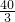 ,
,把点A(0,10)代入a(x-1)2+
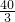 ,得a(0-1)2+
,得a(0-1)2+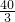 =10,
=10,解得a=-
 ,
,因此抛物线解析式为y=-
 (x-1)2+
(x-1)2+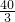 ,
,当y=0时,解得x1=3,x2=-1(不合题意,舍去);
即OB=3米.
故选B.
点评:解答此题的关键是正确建立坐标系,求得函数解析式,再据具体条件利用解析式解决问题.

练习册系列答案
相关题目
 某幢建筑物,从10m高的窗口A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图,如果抛物线的最高点M离墙1m,离地面
某幢建筑物,从10m高的窗口A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图,如果抛物线的最高点M离墙1m,离地面
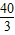 m,
m,
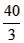 m,则水流落地点B离墙的距离OB是
m,则水流落地点B离墙的距离OB是 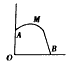
 m,则水流落地点B离墙的距离OB是
m,则水流落地点B离墙的距离OB是