Question

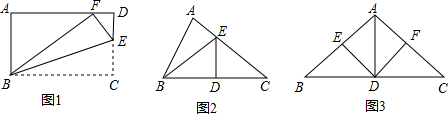
(13分)如图，在△ABC中，AB＝AC＝5，BC＝6，点D为AB边上的一动点(D不与A、B重合)，过D作DE∥BC，交AC于点E．把△ADE沿直线DE折叠，点A落在点A'处．连结BA'，设AD＝x，△ADE的边DE上的高为y．

1.(1) 求出y与x的函数关系式；

2.(2) 若以点A'、B、D为顶点的三角形与△ABC 相似，求x的值；

3.(3) 当x取何值时，△A'DB是直角三角形．

 

Answer 1

 

1.解：(1) 过A点作AM⊥BC，垂足为M，交DE于N点，则BM＝BC＝3，

∵DE∥BC，∴AN⊥DE，即y＝AN．

在Rt△ABM中，AM＝＝4，    …………………………………………………………2分

∵DE∥BC，

∴△ADE∽△ABC，     ……………………………………………………………………………3分

∴＝，

∴＝，

∴y＝(0＜x＜5)． 

2.(2) ∵△A'DE由△ADE折叠得到，

∴AD＝A'D，AE＝A'E，

∵由(1)可得△ADE是等腰三角形，

∴AD＝A'D，AE＝A'E，

∴四边形ADA'E是菱形，         ………………………………5分

∴AC∥D A'，

∴∠BDA'＝∠BAC，又∵∠BAC≠∠ABC，∠BAC≠∠C，

∴∠BDA'≠∠ABC，∠BDA'≠∠C，

∴有且只有当BD＝A'D时，△BDA'∽△BAC，     …………………………………………7分

∴当BD＝A'D，即5－x＝x时，

∴x＝．  

3.(3) 第一种情况：∠BDA'＝90°，

∵∠BDA'＝∠BAC，而∠BAC≠90°，

∴∠BDA'≠90°．          ………………………………………………………………………9分

第二种情况：∠BA'D＝90°，

∵四边形ADA'E是菱形，∴点A'必在DE垂直平分线上，即直线AM上，

∵AN＝A'N＝ y＝，AM＝4，

∴A'M＝|4－x|，

在Rt△BA'M中， A'B2＝BM2＋A'M2＝32＋(4－x)2，

在Rt△BA'D中，A'B2＝BD2＋A'D2＝(5－x)2－x2，

∴ (5－x)2－x2＝32＋(4－x)2，

解得 x＝，x＝0(舍去)．            ……………………………………………………11分

第三种情况：∠A'BD＝90°，

解法一：∵∠A'BD＝90°，∠AMB＝90°，

∴△BA'M∽△ABM，

即＝，∴BA'＝，        ……………………………12分

在Rt△D BA'中，DB2＋A'B2＝A'D2，

(5－x)2＋＝x2，

解得：x＝．        ……………………………………………13分

解法二：∵AN＝A'N＝ y＝，AM＝4，

∴A'M＝|x－4|，

在Rt△BA'M中， A'B2＝BM2＋A'M2＝32＋(x－4)2，

在Rt△BA'D中，A'B2＝ A'D2－BD2＝x2－(5－x)2，

∴ x2－(5－x)2＝32＋(x－4)2，

解得x＝5(舍去)，x＝．        ………………………………………………………13分

综上可知当x＝、x＝时， △A'DB是直角三角形

解析:略