题目内容
已知点O是平面直角坐标系的原点,直线y=﹣x+m+n与双曲线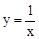 交于两个不同的点A(m,n)(m≥2)和B(p,q).直线y=﹣x+m+n与y轴交于点C,求△OBC的面积S的取值范围.
交于两个不同的点A(m,n)(m≥2)和B(p,q).直线y=﹣x+m+n与y轴交于点C,求△OBC的面积S的取值范围.
 <S≤
<S≤
解析试题分析:先确定直线y=﹣x+m+n与坐标轴的交点坐标,即C点坐标为(0,m+n),D点坐标为(m+n,0),则△OCD为等腰直角三角形,根据反比例函数的对称性得到点A与点B关于直线y=x对称,则B点坐标为(n,m),根据三角形面积公式得到S△OBC= (m+n)•n,然后mn=1,m≥2确定S的范围。
(m+n)•n,然后mn=1,m≥2确定S的范围。
解:如图,C点坐标为(0,m+n),D点坐标为(m+n,0),
则△OCD为等腰直角三角形,
∵点A与点B关于直线y=x对称,∴B点坐标为(n,m)。
∴S=S△OBC= (m+n)•n=
(m+n)•n= mn+
mn+ n2。
n2。
∵点A(m,n)在双曲线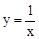 上,
上,
∴ 。∴S=
。∴S= +
+ (
( )2。
)2。
∵m≥2,∴0< ≤
≤ 。∴0<(
。∴0<( )2≤
)2≤ 。
。
∴ <S≤
<S≤ 。
。

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
| 年度 | 2009 | 2010 | 2011 | 2012 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
(2)按照上述函数模型,若2013年已投入技改资金5万元
①预计生产成本每件比2012年降低多少元?
②如果打算在2013年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?
如图,已知∠1=∠2,则下列结论一定成立的是( )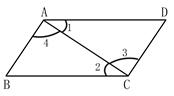
| A.AB//CD | B.AD//BC | C.∠B=∠D | D.∠3=∠4 |
 (m为常数)的图象与反比例函数
(m为常数)的图象与反比例函数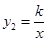 (k为常数,
(k为常数,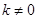 )的图象相交于点 A(1,3).
)的图象相交于点 A(1,3).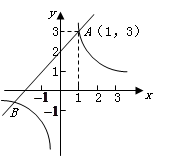
 的坐标;
的坐标;  的自变量
的自变量 的取值范围.
的取值范围. (x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数
(x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数 (x>0)的图象上.
(x>0)的图象上.
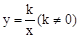 的图象都经过点A(a,2).
的图象都经过点A(a,2).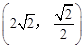 是否在该反比例函数的图象上,请说明理由.
是否在该反比例函数的图象上,请说明理由.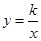 的图象交于A、B两点。
的图象交于A、B两点。