题目内容
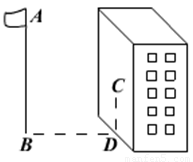
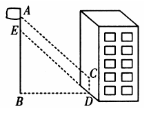
如图，某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙上的影高为2米，求旗杆的高度．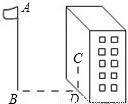
【答案】分析：旗杆的高度=CD+BD所对应的物长，把相关数值代入即可求解．
解答：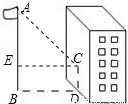
解：过C作CE⊥AB于E，
∵CD⊥BD，AB⊥BD，
∴∠EBD=∠CDB=∠CEB=90°
∴四边形CDBE为矩形，
BD=CE=21，CD=BE=2
设AE=xm．
则1：1.5=x：21，
解得：x=14
故旗杆高AB=AE+BE=14+2=16米．
点评：解决本题的难点在于得到旗杆高度的组成部分．
解答：
解：过C作CE⊥AB于E，∵CD⊥BD，AB⊥BD，
∴∠EBD=∠CDB=∠CEB=90°
∴四边形CDBE为矩形，
BD=CE=21，CD=BE=2
设AE=xm．
则1：1.5=x：21，
解得：x=14
故旗杆高AB=AE+BE=14+2=16米．
点评：解决本题的难点在于得到旗杆高度的组成部分．
练习册系列答案
名校课堂系列答案
相关题目
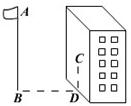24、如图，某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙上的应高为2米，求旗杆的高度．
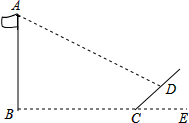如图，某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长2米，在同时刻测量旗杆的影长时，旗杆的影子一部分落在地面上（BC），有一部分落在斜坡上（CD），他测得落在地面上影长为10米，留在斜坡上的影长为2米，∠DCE为45°，则旗杆的高度约为多少米？（参考数据：
