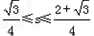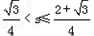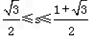题目内容
 如图,
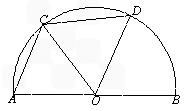
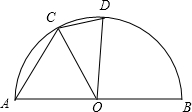
如图, 是半径为1的半圆弧,△AOC为等边三角形,D是
是半径为1的半圆弧,△AOC为等边三角形,D是 上的一动点,则△COD的面积S的最大值是
上的一动点,则△COD的面积S的最大值是
- A.
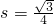
- B.
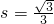
- C.
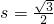
- D.
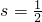
D
分析:根据三角形的面积公式S△COD= CO•ODsin∠COD,因为ab都是圆的半径1,所以sin∠COD的值越大,面积越大进行解答.
CO•ODsin∠COD,因为ab都是圆的半径1,所以sin∠COD的值越大,面积越大进行解答.
解答:S△COD= CO•ODsin∠COD,
CO•ODsin∠COD,
∵CO=OD=1,
∴S△COD= sin∠COD,
sin∠COD,
∵△AOC为等边三角形,
∴∠COB=120°,
∴0°<∠COD<120°,
∴当∠COD=90°时,sin∠COD最大,最大值是1,
∴△COD的面积S的最大值是 .
.
故选D.
点评:本题考查了三角形的面积的求法与锐角三角函数的增减性,熟记面积的求法并判断出∠COD的取值范围是解题的关键.
分析:根据三角形的面积公式S△COD=
 CO•ODsin∠COD,因为ab都是圆的半径1,所以sin∠COD的值越大,面积越大进行解答.
CO•ODsin∠COD,因为ab都是圆的半径1,所以sin∠COD的值越大,面积越大进行解答.解答:S△COD=
 CO•ODsin∠COD,
CO•ODsin∠COD,∵CO=OD=1,
∴S△COD=
 sin∠COD,
sin∠COD,∵△AOC为等边三角形,
∴∠COB=120°,
∴0°<∠COD<120°,
∴当∠COD=90°时,sin∠COD最大,最大值是1,
∴△COD的面积S的最大值是
 .
.故选D.
点评:本题考查了三角形的面积的求法与锐角三角函数的增减性,熟记面积的求法并判断出∠COD的取值范围是解题的关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
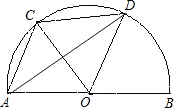 如图,
如图,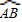 是半径为1的半圆弧,△AOC为等边三角形,D是
是半径为1的半圆弧,△AOC为等边三角形,D是 上的一动点,则△COD的面积S的最大值是( )
上的一动点,则△COD的面积S的最大值是( )

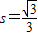


 是半径为1的半圆弧,△AOC为等边三角形,D是
是半径为1的半圆弧,△AOC为等边三角形,D是 上的一动点,则三角形AOD的面积s的取值范围是 .
上的一动点,则三角形AOD的面积s的取值范围是 .
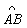 是半径为1的半圆弧,△AOC为等边三角形,D是
是半径为1的半圆弧,△AOC为等边三角形,D是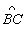 上的一动点,则四边形AODC的面积s的取值范围是=
上的一动点,则四边形AODC的面积s的取值范围是=