��Ŀ����
����Ŀ����ͼ1��������OABC�ı߳�Ϊ12����A��C�ֱ���x�ᡢy����������ϣ�˫����y��![]() ��x��0�����BC��AD�ֱ��ڵ�D��E����BD��AE.
��x��0�����BC��AD�ֱ��ڵ�D��E����BD��AE.


��1����k��ֵ��
��2����ͼ2������NΪ˫����y��![]() ��������OABC�ڲ�һ���㣬����N��y��Ĵ��ߣ���AC�ڵ�F����AB�ڵ�G������F��x��Ĵ��߽�Ϊ˫����y��
��������OABC�ڲ�һ���㣬����N��y��Ĵ��ߣ���AC�ڵ�F����AB�ڵ�G������F��x��Ĵ��߽�Ϊ˫����y��![]() �ڵ�M.���N��������Ϊn
�ڵ�M.���N��������Ϊn
����n��8����֤����BMN��ֱ�������Σ�
����ȥ�����е����� ��n��8���� ��BMN�Ƿ���Ϊֱ�������Σ���֤����Ľ���.
���𰸡���1��![]() ;��2����֤��������; �ڡ�BMN��Ϊ��ֱ�������Σ����ɼ�����.
;��2����֤��������; �ڡ�BMN��Ϊ��ֱ�������Σ����ɼ�����.
�������������������1����BD=AD=a����ʾ��E,D��������꣬�������㶼��˫�����ϣ��������k��ֵ��(2)�ֱ����BM��BN��MN�ij��ȣ����ݹ��ɶ������涨������֤�ã���3���ú�n�Ĵ���ʽ��ʾ��GM��MB��DE��BD�ij��ȣ�����������ȵõ���GBM=��EBD���ٸ�����EBD+��CBE=90������֤��.
���������
��1����BD=AD=a����E(12,a),D(12-a,12),
��˫����y��![]() ��x��0�����BC��AD�ֱ��ڵ�D��E��
��x��0�����BC��AD�ֱ��ڵ�D��E��
�� ,
,
��ã� ![]()
���ϣ�k��ֵ��72.
��2��������BMN��
BM![]() ��BN
��BN![]() ��
��
MN![]() ��
��
��MN2=BM2+BN2��
���BMN��ֱ��������
�ڡ�BMN��Ϊ��ֱ�������Σ��������£�
��N��������![]() ��n��,F��12-n��n����M(12-n��
��n��,F��12-n��n����M(12-n�� ![]() )
)
�� GM=![]() ,MB=n,DE=
,MB=n,DE=![]() ,BD=12-n,
,BD=12-n,
����BED����  ��
��
����BDE���� 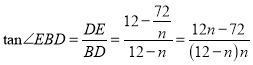 ��
��
���GBM=��EBD,
�ߡ�EBD+��CBE=90��,
���GBM+��CBE=90��,
����BMN��Ϊ��ֱ��������.
�㾦: �����Ƿ������������ۺ��⣬�����������ε����ʣ�����������ͼ���ϵ����������������ϵ������Ӧ���Լ���ֱ�������ε�Ӧ�õȣ�
