题目内容
已知x1+x2=-b，x1•x2=c，用b、c的式子表示(x1-x2)2，并求当b=4，c=3时，(x1-x2)2的值．
分析：先把要求的式子根据完全平方公式求出（x1-x2）2=（x1+x2）2-4x1x2，然后把x1+x2=-b，x1•x2=c代入求出式子，最后把b=4，c=3代入即可．
解答：解：∵（x1-x2）2=（x1+x2）2-4x1x2，
又∵x1+x2=-b，x1•x2=c，
∴（x1-x2）2=（-b）2-4c=b2-4c，
把b=4，c=3代入上式得：
原式=42-4×3=16-12=4，
∴(x1-x2)2的值4．
又∵x1+x2=-b，x1•x2=c，
∴（x1-x2）2=（-b）2-4c=b2-4c，
把b=4，c=3代入上式得：
原式=42-4×3=16-12=4，
∴(x1-x2)2的值4．
点评：本题考查了完全平方公式，解题的关键是熟记完全平方公式（a+b）2=a2+2ab+b2，题目比较典型．
练习册系列答案
阅读快车系列答案
相关题目
=
.
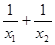