题目内容
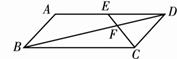
如图,在平行四边形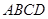 中,以点
中,以点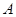 为圆心,
为圆心,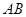 为半径的圆,交
为半径的圆,交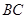 于点
于点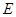 .
.
(1)求证: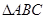 ≌
≌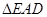 ;
;
(2)如果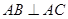 ,
,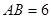 ,
,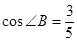 ,求
,求 的长.
的长.
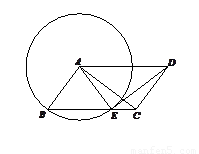
【答案】
(1)证明见解析(2)
【解析】(1)∵四边形 是平行四边形
是平行四边形
∴ ,
, ∥
∥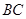
∴
∵ 与
与 为圆的半径
为圆的半径
∴
∴
∴
∴△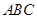 ≌△
≌△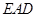 1分
1分
(2)∵


∴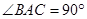
∴在直角三角形△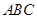 中,
中,
∵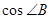 =
= ,
,
∴
过圆心 作
作 ,
, 为垂足
为垂足
∴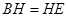
∴在直角三角形△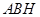 中,
中,
∴
∴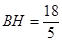
∴
∴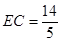
(1)根据平行四边形的性质得出AD=BC,根据圆的半径相等可得出AB=AE,结合等腰三角形的性质和平行线的性质可得出∠B=∠EAD,从而利用SAS可证得结论.
(2)在RT△ABC中,可求出BC,过圆心A作AH⊥BC,垂足为H,则BH=HE,则结合cos∠B的值,可求出BH、EH的长度,继而根据EC=BC-BE即可得出答案.
|

练习册系列答案
相关题目
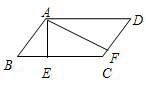 19、如图,在平行四边形中,AE⊥BC于E,AF⊥CD于F,∠EAF=60°,求平行四边形各个内角的度数.
19、如图,在平行四边形中,AE⊥BC于E,AF⊥CD于F,∠EAF=60°,求平行四边形各个内角的度数.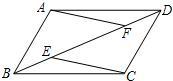 22、如图,在平行四边形中,点E,F是对角线BD上两点,且BF=DE.
22、如图,在平行四边形中,点E,F是对角线BD上两点,且BF=DE. (2013•宜春模拟)如图,在平行四边形中挖去一个矩形,在请用无刻度的直尺,准确作出一条直线将剩下图形的面积平分.(保留作图痕迹)
(2013•宜春模拟)如图,在平行四边形中挖去一个矩形,在请用无刻度的直尺,准确作出一条直线将剩下图形的面积平分.(保留作图痕迹) 中,
中,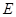 为
为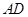 的中点,
的中点,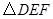 的周长为1,则
的周长为1,则