题目内容
如图,AB是⊙O的直径,点C是BA延长线上一点,CD切⊙O于点D,CA=1,CD是⊙O半径的| 3 |
(1)求⊙O的半径R;
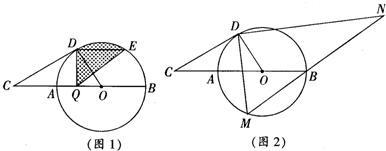
(2)如图1,弦DE∥CB,动点Q从A出发沿直径AB向B运动的过程中,图中阴影部分的面积是否发生变化,若发生变化,请你说明理由;若不发生变化,请你求出阴影部分的面积;
(3)如图2,动点M从A出发,在⊙O上按逆时针方向向B运动.连接DM,过D作DM的垂线,与MB的延长线交于点N,当点M运动到什么位置时,DN取到最大值?求此时动点M所经过的弧长.
分析:(1)由题意,CD是⊙O半径的
倍,CA=1,在直角△CDO中,根据勾股定理CD2+OD2=CO2,代入即可求出;
(2)由DE∥CB,可知,动点Q从A出发沿直径AB向B运动的过程中,△DEQ的面积不变,则阴影部分的面积不变;当点Q运动到O点时,则∠DOE=60°,即可求出阴影部分的面积;
(3)如图,连接AD、BD,当DM过圆心O时,DN取到最大值;易证△ADB∽△MDN,由已知,可求得,AD=1,BD=
,所以,DN=
DM,此时,∠AOM=120°,即可求得
的长.
| 3 |
(2)由DE∥CB,可知,动点Q从A出发沿直径AB向B运动的过程中,△DEQ的面积不变,则阴影部分的面积不变;当点Q运动到O点时,则∠DOE=60°,即可求出阴影部分的面积;
(3)如图,连接AD、BD,当DM过圆心O时,DN取到最大值;易证△ADB∽△MDN,由已知,可求得,AD=1,BD=
| 3 |
| 3 |
 |
| AM |
解答:解:(1)∵CD切⊙O于点D,
∴三角形CDO是直角三角形,
∵CA=1,CD是⊙O半径的
倍,
∴在直角△CDO中,CD2+OD2=CO2,
则,(
R)2+R2=(1+R)2,
∴R=1;
(2)∵DE∥CB,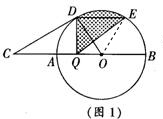
∴动点Q从A出发沿直径AB向B运动的过程中,△DEQ的底DE不变,底DE上的高不变,
∴△DEQ的面积不变,则阴影部分的面积不变;
由OD=1,CO=2,
∴∠C=30°,则∠COD=60°,
∴∠ODE=60°,
∵∠ODE=∠OED,
∴∠OED=60°
∴∠DOE=60°,
∴S阴影=
×πR2=
π;
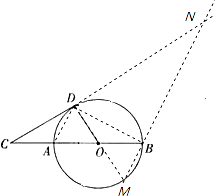
(3)如图,连接AD、BD,
∴∠DAB=∠DMN,又∠ADB=∠MDN=90°,
∴△ADB∽△MDN,
又AD=1,AB=2,
∴BD=
,
∴
=
=
,
∴DN=
DM,
∴当DM为最大值,即DM过圆心O时,DN取到最大值;
∵∠AOD=60°,
∴∠AOM=120°,
∴
=
×2πR=
π.
∴三角形CDO是直角三角形,
∵CA=1,CD是⊙O半径的
| 3 |
∴在直角△CDO中,CD2+OD2=CO2,
则,(
| 3 |
∴R=1;
(2)∵DE∥CB,

∴动点Q从A出发沿直径AB向B运动的过程中,△DEQ的底DE不变,底DE上的高不变,
∴△DEQ的面积不变,则阴影部分的面积不变;
由OD=1,CO=2,
∴∠C=30°,则∠COD=60°,
∴∠ODE=60°,
∵∠ODE=∠OED,
∴∠OED=60°
∴∠DOE=60°,
∴S阴影=
| 60° |
| 360° |
| 1 |
| 6 |

(3)如图,连接AD、BD,
∴∠DAB=∠DMN,又∠ADB=∠MDN=90°,
∴△ADB∽△MDN,
又AD=1,AB=2,
∴BD=
| 3 |
∴
| DN |
| DM |
| BD |
| AD |
| 3 |
∴DN=
| 3 |
∴当DM为最大值,即DM过圆心O时,DN取到最大值;
∵∠AOD=60°,
∴∠AOM=120°,
∴
 |
| AM |
| 120° |
| 360° |
| 2 |
| 3 |
点评:本题考查了切线的性质、扇形面积的计算、弧长的计算及直角三角形的知识,作辅助线连接圆心和切点,利用垂直构造直角三角形解决是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( ) 0.1平方米)
0.1平方米)

 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为