题目内容
【题目】在直角坐标系中,点O为坐标原点,A(1,1),B(1,3),将线段AB平移到直线AB的右边得到线段CD(点C与点A对应,点D与点B对应),点D的坐标为(m,n),且m>1.
(1)如图1,当点C坐标为(2,0)时,请直接写出三角形BCD的面积: ;
(2)如图2,点E是线段CD延长线上的点,∠BDE的平分线DF交射线AB于点F.求证![]() ;
;
(3)如图3,线段CD运动的过程中,在(2)的条件下,n=4.
①当![]() 时,在直线AB上点P,满足三角形PBC的面积等于三角形CDF的面积,请直接写出点P的坐标: ;
时,在直线AB上点P,满足三角形PBC的面积等于三角形CDF的面积,请直接写出点P的坐标: ;
②在x轴上的点Q,满足三角形QBC的面积等于三角形CDF的面积的2倍,请直接写出点Q的坐标: .(用含m的式子表示).

【答案】(1)1;(2)证明见解析;(3)①P1(1,5), P2(1,1);②Q(2![]() m,0).
m,0).
【解析】分析:(1)根据点A和点C的坐标得出平移的方向和距离,进而得出点D的坐标,根据三角形的面积公式即可得出答案;
(2)根据平移的性质得出AB∥CD,AC∥BD,根据平行线的性质可得∠AFD =∠FDE,∠C =∠BDE,根据角平分线的定义等量代换即可得出结论;
(3)①由题意D(4,4),C(4,2),所以CD=2,进而可以求出△CDF的面积,然后根据△PBC的面积和△CDF的面积相等求出PB的长,即可得出P的坐标;
②由题意得:C(m,2),D(m,4),则CD=2,
△CDF的CD边上的高为m-1,
进而可以用m表示出△CDF的面积,
设Q(x,0),
分x<1,1<x<m,x>m三种情况表示出△BCQ的面积,
然后根据三角形QBC的面积等于三角形CDF的面积的2倍列出方程求出x即可.
详解:(1)∵A(1,1)平移至点C(2,0),
∴点B(1,3)的对应点D(2,2),
∴CD=2,B到CD的距离为1,
所以△BCD的面积为:![]() ×2×1=1.
×2×1=1.
故答案为:1;
(2)证明:∵ 线段AB平移得到线段CD(点C与点A对应,点D与点B对应),
∴ AB∥CD,AC∥BD.
∴ ∠AFD =∠FDE,∠C =∠BDE.
∵ DF是∠BDE的角平分线,
∴ ∠BDE =2∠FDE .
∴ ∠BDE =2∠AFD.
∴ ∠C =2∠AFD.
(3)①由题意D(4,4),C(4,2),
所以CD=2,直线AB与CD间的距离为3,
∴S△CDF=![]() ×2×3=3,
×2×3=3,
∴S△PBC=![]() PB·3=3,
PB·3=3,
∴PB=2,
∵点P在直线AB上,且AB⊥x轴,
∴点P的坐标为(1,5)或(1,1).
故答案为:P1(1,5), P2(1,1);
②由题意得:C(m,2),D(m,4),则CD=2,
△CDF的CD边上的高为m-1,
∴S△CDF=![]() ×2(m-1)=m-1,
×2(m-1)=m-1,
设Q(x,0),
当x<1时,如图所示:
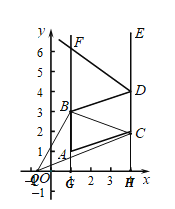
S△QBC=S梯形BGHC+S△BQG-S△QCH
=![]() (2+3)(m-1)+
(2+3)(m-1)+ ![]() (1-x)·3-
(1-x)·3-![]() (m-x)·2
(m-x)·2
=
解得:x=2-m,
∴点Q的坐标为(2-m,0);
当1<x<m时,如图所示:
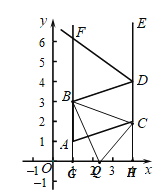
S△QBC=S梯形BGHC-S△BQG-S△QCH
=![]() (2+3)(m-1)-
(2+3)(m-1)- ![]() (x-1)·3-
(x-1)·3-![]() (m-x)·2
(m-x)·2
=![]() =2(1-m),
=2(1-m),
解得:x=2-m,
∴点Q的坐标为(2-m,0);
当x>m时,如图所示:
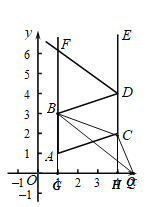
S△QBC=S梯形BGHC-S△BQG+S△QCH
=![]() (2+3)(m-1)-
(2+3)(m-1)- ![]() (x-1)·3-
(x-1)·3-![]() (x-m)·2
(x-m)·2
=![]() =2(1-m),
=2(1-m),
解得:x=2-m,
∴点Q的坐标为(2-m,0);
综上点Q的坐标为(2-m,0).
故答案为:(2-m,0).
三种情况表示出△BCQ的面积,
然后根据三角形QBC的面积等于三角形CDF的面积的2倍列出方程求出x即可.
Q(2-m, 0)或Q(7m-6,0).

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案


