题目内容
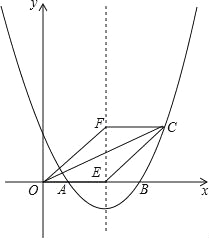
【题目】如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).
(1)求抛物线的解析式及对称轴;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标.

【答案】(1)抛物线的解析式为y=![]() .
.
抛物线的对称轴为x=﹣![]() .
.
(2)点C的坐标为(5,2).
【解析】
试题分析:(1)由点A、B的坐标利用待定系数法即可求出抛物线的解析式,再由抛物线的对称轴为x=﹣![]() ,代入数据即可得出结论;
,代入数据即可得出结论;
(2)由平行四边形的性质即可得出点C的横坐标,代入抛物线解析式中即可得出点C的坐标.
试题解析:(1)将点A(1,0)、B(4,0)代入y=ax2+bx+2中,
得:![]() ,解得:
,解得: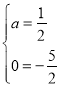 ,
,
∴抛物线的解析式为y=![]() .
.
抛物线的对称轴为x=﹣![]() =
=![]() .
.
(2)∵OECF是平行四边形,OE=![]() ,
,
∴FC=![]() ,
,
∴C点横坐标x=OE+FC=5,
令y=![]() 中x=5,则y=2,
中x=5,则y=2,
∴点C的坐标为(5,2).

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目