题目内容
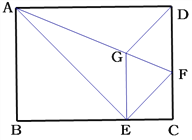
【题目】如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．
(1)求证：四边形EFDG是菱形；
(2)探究线段EG，GF，AF之间的数量关系，并说明理由；
(3)若AG=6，EG=2
，求BE的长．
【答案】（1）详见解析；（2）
.
【解析】试题分析：（1）根据已知条件易证
，即可判定四边形EFDG是菱形；（2）连接ED交AF于点H，根据菱形的性质可得
在证明RtFEH∽RtFAE,根据相似三角形的性质可得
，代入数值即可求得GF的长，再求得AD、DE的长，最后再判定RtADF∽RtDCE,即可得
，带入数值即可得结论.
试题解析：由折叠的性质可得
∴四边形EFDG是菱形．
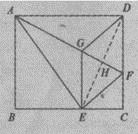
（2）连接ED交AF于点H，
∵四边形EFDG是菱形，
∴RtFEH∽RtFAE,
∵AG=6，EG=2
，EG2=
，∴（2）2=
∴RtADF∽RtDCE
练习册系列答案
通城学典默写能手系列答案
相关题目
