题目内容
下列说法:①面积相等,且有一边相等的两个的三角形全等;②斜边和直角边对应相等的两个直角三角形全等;③全等图形的面积相等;④所有周长相等的三角形都全等,正确的有
- A.1个
- B.2个
- C.3个
- D.4个
B
分析:①利用两三角形等底等高面积相等,但形状可以不相同,判断即可;②利用HL定理进行判定即可;
③利用全等三角形的性质得出即可;④利用特殊值法举例说明即可.
解答:①面积相等,且有一边相等的两个的三角形全等;
如图所示:
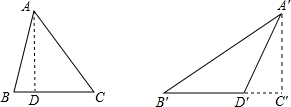
在△ABC和△A′B′C′中,
当BC=B′C′,高AD=高A′D′,
此时两三角形面积相等,且有一边相等,但是两个三角形明显不全等,故此选项错误;
②斜边和直角边对应相等的两个直角三角形全等;
根据HL定理即可得出斜边和直角边对应相等的两个直角三角形全等,故此选项正确;
③全等图形的面积相等;
根据全等图形的性质得出,此选项正确;
④所有周长相等的三角形都全等,
当两三角形的边长分别为:3,3,4和2,4,4时,两三角形不可能全等,故此选项错误;
故正确的有2个,
故选:B.
点评:此题主要考查了全等三角形的性质和判定以及利用特殊值法判定真假命题,熟练利用三角形的性质举出特例是解题关键.
分析:①利用两三角形等底等高面积相等,但形状可以不相同,判断即可;②利用HL定理进行判定即可;
③利用全等三角形的性质得出即可;④利用特殊值法举例说明即可.
解答:①面积相等,且有一边相等的两个的三角形全等;
如图所示:
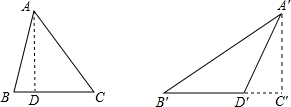
在△ABC和△A′B′C′中,
当BC=B′C′,高AD=高A′D′,
此时两三角形面积相等,且有一边相等,但是两个三角形明显不全等,故此选项错误;
②斜边和直角边对应相等的两个直角三角形全等;
根据HL定理即可得出斜边和直角边对应相等的两个直角三角形全等,故此选项正确;
③全等图形的面积相等;
根据全等图形的性质得出,此选项正确;
④所有周长相等的三角形都全等,
当两三角形的边长分别为:3,3,4和2,4,4时,两三角形不可能全等,故此选项错误;
故正确的有2个,
故选:B.
点评:此题主要考查了全等三角形的性质和判定以及利用特殊值法判定真假命题,熟练利用三角形的性质举出特例是解题关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目