题目内容
已知:在坐标平面内A(0,0)、B(12,0)、C(12,6)、D(0,6),点Q、P分别沿DA、AB从D、A向A、B以1单 位/秒,2单位/秒的速度移动,同时出发,t表示移动时间(0≤t≤6).
位/秒,2单位/秒的速度移动,同时出发,t表示移动时间(0≤t≤6).(1)写出△PQA的面积S与t的函数关系式.
(2)四边形APCQ的面积与t有关吗?说明理由.
(3)t等于多少时,△APQ为轴对称图形.
(4)PQ能否与AC垂直?若能,求出直线PQ的解析式;若不能,说明理由.
分析:(1)根据A,B,C,D四点的坐标可知:四边形ABCD是个矩形,可根据P,Q的速度用时间t表示出AQ,AP的长,进而用三角形的面积公式得出S与t的函数关系式;
(2)连接AC,四边形APCQ的面积可以分成△AQC和△APC两部分,S△AQC=
(6-t)•12=36-6t,S△APC=
•2t•6=6t,因此四边形APCQ的面积等于36与t的大小没有关系;
(3)要使△APQ为轴对称图形,只有一种情况即AP=AQ时,△APQ为等腰直角三角形,那么AP=AQ,即6-t=2t,因此t=3.此时等腰直角三角形的对称轴正好是第一象限的角平分线即y=x;
(4)假设PQ⊥AC,根据两角对应相等,两三角形相似,证出△ABC∽△QAP,由相似三角形对应边成比例列出比例式,如果能够求出符合题意的t值,说明PQ能与AC垂直,从而运用待定系数法求出直线PQ的解析式;如果不能够求出符合题意的t值,说明PQ不能与AC垂直.
(2)连接AC,四边形APCQ的面积可以分成△AQC和△APC两部分,S△AQC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)要使△APQ为轴对称图形,只有一种情况即AP=AQ时,△APQ为等腰直角三角形,那么AP=AQ,即6-t=2t,因此t=3.此时等腰直角三角形的对称轴正好是第一象限的角平分线即y=x;
(4)假设PQ⊥AC,根据两角对应相等,两三角形相似,证出△ABC∽△QAP,由相似三角形对应边成比例列出比例式,如果能够求出符合题意的t值,说明PQ能与AC垂直,从而运用待定系数法求出直线PQ的解析式;如果不能够求出符合题意的t值,说明PQ不能与AC垂直.
解答:解:(1)∵AP=2t,DQ=t,
∴AQ=AD-DQ=6-t,
∴S△APQ=
AP•AQ=
•2t(6-t)=-t2+6t,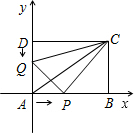
∴S=-t2+6t;
(2)连接AC.
∵S四边形APCQ=S△AQC+S△APC=
(6-t)•12+
•2t•6=36,
∴四边形APGQ的面积与t无关;
(3)当且仅当AQ=AP,即6-t=2t,t=2时,△AQP是等腰直角三角形,从而是轴对称图形.
故当t=2时,△APQ为轴对称图形;
(4)假设PQ⊥AC,则∠CAB=∠PQA=90°-∠APQ,
又∵∠ABC=∠QAP=90°,
∴△ABC∽△QAP,
∴AB:QA=BC:AP,
∴
=
,
解得t=
.
∴AP=2t=
,AQ=6-t=
.
设直线PQ的解析式为y=kx+b,
∵P(
,0)、Q(0,
)在此直线上,
∴
,
解得
.
∴直线PQ的解析式为y=-2x+
.
∴AQ=AD-DQ=6-t,
∴S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |

∴S=-t2+6t;
(2)连接AC.
∵S四边形APCQ=S△AQC+S△APC=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形APGQ的面积与t无关;
(3)当且仅当AQ=AP,即6-t=2t,t=2时,△AQP是等腰直角三角形,从而是轴对称图形.
故当t=2时,△APQ为轴对称图形;
(4)假设PQ⊥AC,则∠CAB=∠PQA=90°-∠APQ,
又∵∠ABC=∠QAP=90°,
∴△ABC∽△QAP,
∴AB:QA=BC:AP,
∴
| 12 |
| 6-t |
| 6 |
| 2t |
解得t=
| 6 |
| 5 |
∴AP=2t=
| 12 |
| 5 |
| 24 |
| 5 |
设直线PQ的解析式为y=kx+b,
∵P(
| 12 |
| 5 |
| 24 |
| 5 |
∴
|
解得
|
∴直线PQ的解析式为y=-2x+
| 24 |
| 5 |
点评:本题考查了矩形的性质、图形面积的求法、轴对称图形、相似三角形的判定与性质及待定系数法求一次函数的解析式等知识,综合性较强,有一定难度.

练习册系列答案
相关题目
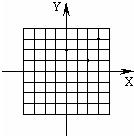 5、已知△ABC在坐标平面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以B为位似中心,画出与△ABC相似(与图形同向),且相似比是3的三角形,它的三个对应顶点的坐标分别是
5、已知△ABC在坐标平面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以B为位似中心,画出与△ABC相似(与图形同向),且相似比是3的三角形,它的三个对应顶点的坐标分别是 23、已知△ABC在坐标平面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以B为位似中心,画出△Α1Β1С1与△ABC相似(与图形同向),且相似比是2的三角形,它的三个对应顶点的坐标分别是:
23、已知△ABC在坐标平面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以B为位似中心,画出△Α1Β1С1与△ABC相似(与图形同向),且相似比是2的三角形,它的三个对应顶点的坐标分别是: 位/秒,2单位/秒的速度移动,同时出发,t表示移动时间(0≤t≤6).
位/秒,2单位/秒的速度移动,同时出发,t表示移动时间(0≤t≤6).