题目内容
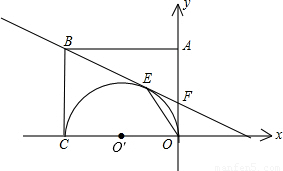
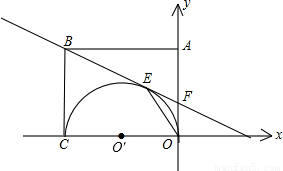
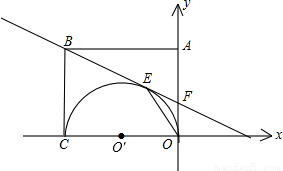
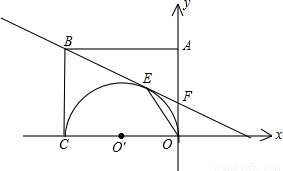
(2001•江西)如图,矩形OABC的两边OC、OA分别是x轴和y轴上,过点B的直线切以OC为直径的半圆O′于点E,交y轴于点F,连接OE,且已知C(-6,0),F(0,2).(1)求EF的长;
(2)求经过B、F两点的直线的解析式;
(3)求tan∠EOF的值.
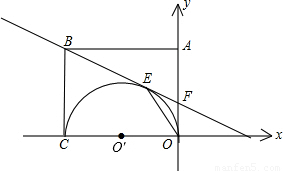
【答案】分析:(1)由题意知FO是圆的切线,则由切线长定理知,EF=OF=2;
(2)由题意设出直线BF的解析式,由O点到直线距离为3,求得B点的坐标,设E(a,2-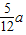 ),由勾股定理求得a的值,进而得到直线BF的解析式;
),由勾股定理求得a的值,进而得到直线BF的解析式;
(3)作EM垂直于y轴于点M,由正切的概念求得tan∠EOF的值.
解答:解:(1)由题意知,AO⊥CO,CO是半圆的直径,
∴FO是半圆的切线,
∵AB是切线,点E是切点,
∴EF=OF=2;

(2)已知C(-6,0),设点B(-6,b),F(0,2),
∴BF直线解析式为:y=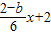 ,
,
∵OE⊥BF,
∴O点到直线距离为3,
又∵O′(-3,0),
∴3=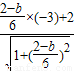 ,
,
∴b= ,
,
∴B(-6, ),
),
设E(a,2-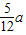 ),
),
又∵|OE|=3,
∴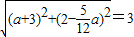 ,
,
∴a=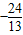 ,
,
∴E(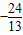 ,
, ),
),
∴BF直线解析式为:y= 把b=
把b= 代入,得:
代入,得:
y=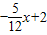 ;
;
(3)由图形几何关系,作EM垂直于y轴于点M,
∴tan∠EOF=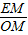 =
= =
= .
.
点评:此题主要考查一次函数的基本性质及圆的性质,直线与圆相切的问题,巧妙设点从而减少未知量,还考查了学生的计算能力.
(2)由题意设出直线BF的解析式,由O点到直线距离为3,求得B点的坐标,设E(a,2-
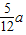 ),由勾股定理求得a的值,进而得到直线BF的解析式;
),由勾股定理求得a的值,进而得到直线BF的解析式;(3)作EM垂直于y轴于点M,由正切的概念求得tan∠EOF的值.
解答:解:(1)由题意知,AO⊥CO,CO是半圆的直径,
∴FO是半圆的切线,
∵AB是切线,点E是切点,
∴EF=OF=2;

(2)已知C(-6,0),设点B(-6,b),F(0,2),
∴BF直线解析式为:y=
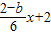 ,
,∵OE⊥BF,
∴O点到直线距离为3,
又∵O′(-3,0),
∴3=
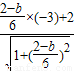 ,
,∴b=
 ,
,∴B(-6,
 ),
),设E(a,2-
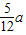 ),
),又∵|OE|=3,
∴
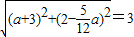 ,
,∴a=
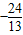 ,
,∴E(
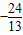 ,
, ),
),∴BF直线解析式为:y=
 把b=
把b= 代入,得:
代入,得:y=
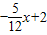 ;
;(3)由图形几何关系,作EM垂直于y轴于点M,
∴tan∠EOF=
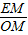 =
= =
= .
.点评:此题主要考查一次函数的基本性质及圆的性质,直线与圆相切的问题,巧妙设点从而减少未知量,还考查了学生的计算能力.

练习册系列答案
相关题目