题目内容
若x2-mx-15=(x+3)(x+n),则nm的值为
- A.-5
- B.2
- C.25
- D.-25
C
分析:将原式展开,然后根据对应项系数相等列式解出m、n的值,再代入计算即可.
解答:原式可化为x2-mx-15=x2+(3+n)x+3n,
∴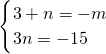 ,
,
解得 ,
,
∴nm=(-5)2=25.
故选C.
点评:本题考查了因式分解与多项式的乘法是互为逆运算的性质,根据对应项系数相等列出等式是解本题的关键.
分析:将原式展开,然后根据对应项系数相等列式解出m、n的值,再代入计算即可.
解答:原式可化为x2-mx-15=x2+(3+n)x+3n,
∴
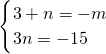 ,
,解得
 ,
,∴nm=(-5)2=25.
故选C.
点评:本题考查了因式分解与多项式的乘法是互为逆运算的性质,根据对应项系数相等列出等式是解本题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目