题目内容
设方程组
|
|
|
| 1 |
| x1 |
| 1 |
| x2 |
分析:首先运用代入消元法从方程组中得到关于x的方程,进一步根据一元二次方程根与系数的关系进行求解则可.
解答:解:把y=2x-1代入方程①,得x2-x-2x+1=0,x2-3x+1=0,
∴x1x2=1,x1+x2=3,
∴
+
=
=3,
y1y2=(2x1-1)(2x2-1)=4x1x2-2(x1+x2)+1=4-6+1=-1.
∴x1x2=1,x1+x2=3,
∴
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1•x2 |
y1y2=(2x1-1)(2x2-1)=4x1x2-2(x1+x2)+1=4-6+1=-1.
点评:本题考查了一元二次方程根与系数的关系,能够把方程组的问题运用消元法转化为一元二次方程中的问题进行求解,熟练运用根与系数的关系是解题的关键.

练习册系列答案
相关题目
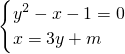 的解是
的解是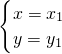 ,
,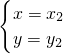 ,x1≠x2.
,x1≠x2. 的解是
的解是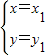 ,
,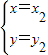 ,x1≠x2.
,x1≠x2.