题目内容
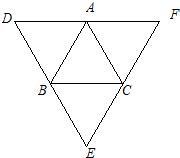
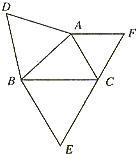
已知△ABC，分别以AB，AC为边，向形外作等边三角形ABD和ACE，连接BE，DC，其中，则△ADC≌△ABE的根据是
- A.SSS
- B.SAS
- C.ASA
- D.AAS
B
分析：考查三角形全等的判定定理，有AAS，SSS，ASA，SAS四种．根据题意，要证明△ADC≌△ABE，还差一对对应边或者一对对应角（夹角），所以，要证明△ADC≌△ABE就要去求证一对对应边相等或者一对对应角（夹角）相等．
解答：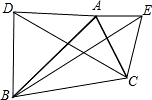
解：∵△ABD和△ACE都是等边三角形，
∴AD=AB，AC=AE，∠DAB=∠EAC=60°，
∴∠DAB+∠BAC=∠EAC=60°+∠BAC，即∠DAC=∠BAE，
∴△ADC≌△ABE （SAS）．
故选B．
点评：本题考查了三角形全等的判定方法；注意对三角形全等判定的应用；先根据已知的条件或已证的结论来证明三角形全等．
分析：考查三角形全等的判定定理，有AAS，SSS，ASA，SAS四种．根据题意，要证明△ADC≌△ABE，还差一对对应边或者一对对应角（夹角），所以，要证明△ADC≌△ABE就要去求证一对对应边相等或者一对对应角（夹角）相等．
解答：
解：∵△ABD和△ACE都是等边三角形，∴AD=AB，AC=AE，∠DAB=∠EAC=60°，
∴∠DAB+∠BAC=∠EAC=60°+∠BAC，即∠DAC=∠BAE，
∴△ADC≌△ABE （SAS）．
故选B．
点评：本题考查了三角形全等的判定方法；注意对三角形全等判定的应用；先根据已知的条件或已证的结论来证明三角形全等．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
