题目内容
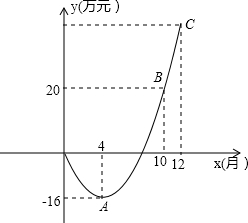 (2013•大丰市二模)某电子科技公司开发一种新产品,公司对经营的盈亏情况每月最后一天结算1次.在1~12月份中,公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数关系式y=a(x-h)2+k,二次函数y=a(x-h)2+k的一部分图象如图所示,点A为抛物线的顶点,且点A、B、C的横坐标分别为4、10、12,点A、B的纵坐标分别为-16、20.
(2013•大丰市二模)某电子科技公司开发一种新产品,公司对经营的盈亏情况每月最后一天结算1次.在1~12月份中,公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数关系式y=a(x-h)2+k,二次函数y=a(x-h)2+k的一部分图象如图所示,点A为抛物线的顶点,且点A、B、C的横坐标分别为4、10、12,点A、B的纵坐标分别为-16、20.(1)试确定函数关系式y=a(x-h)2+k;
(2)分别求出前9个月公司累计获得的利润以及10月份一个月内所获得的利润;
(3)在前12个月中,哪个月该公司一个月内所获得的利润最多?最多利润是多少万元?
分析:(1)根据题意此抛物线的顶点坐标为(4,-16),设出抛物线的顶点式,把(10,20)代入即可求出a的值,把a的值代入抛物线的顶点式中即可确定出抛物线的解析式;
(2)相邻两个月份的总利润的差即为某月利润.
(3)根据前x个月内所获得的利润减去前x-1个月内所获得的利润,再减去16即可表示出第x个月内所获得的利润,为关于x的一次函数,且为增函数,得到x取最大为12时,把x=12代入即可求出最多的利润.
(2)相邻两个月份的总利润的差即为某月利润.
(3)根据前x个月内所获得的利润减去前x-1个月内所获得的利润,再减去16即可表示出第x个月内所获得的利润,为关于x的一次函数,且为增函数,得到x取最大为12时,把x=12代入即可求出最多的利润.
解答:解:(1)根据题意可设:y=a(x-4)2-16,
当x=10时,y=20,
所以a(10-4)2-16=20,解得a=1,
所求函数关系式为:y=(x-4)2-16.-------(4分)
(2)当x=9时,y=(9-4)2-16=9,所以前9个月公司累计获得的利润为9万元,
又由题意可知,当x=10时,y=20,而20-9=11,
所以10月份一个月内所获得的利润11万元.---------(4分)
(3)设在前12个月中,第n个月该公司一个月内所获得的利润为s(万元)
则有:s=(n-4)2-16-[(n-1-4)2-16]=2n-9,
因为s是关于n的一次函数,且2>0,s随着n的增大而增大,
而n的最大值为12,所以当n=12时,s=15,
所以第12月份该公司一个月内所获得的利润最多,最多利润是15万元.--(4分)
当x=10时,y=20,
所以a(10-4)2-16=20,解得a=1,
所求函数关系式为:y=(x-4)2-16.-------(4分)
(2)当x=9时,y=(9-4)2-16=9,所以前9个月公司累计获得的利润为9万元,
又由题意可知,当x=10时,y=20,而20-9=11,
所以10月份一个月内所获得的利润11万元.---------(4分)
(3)设在前12个月中,第n个月该公司一个月内所获得的利润为s(万元)
则有:s=(n-4)2-16-[(n-1-4)2-16]=2n-9,
因为s是关于n的一次函数,且2>0,s随着n的增大而增大,
而n的最大值为12,所以当n=12时,s=15,
所以第12月份该公司一个月内所获得的利润最多,最多利润是15万元.--(4分)
点评:本题考查了二次函数的应用,主要考查学生会利用待定系数法求函数的解析式,灵活运用二次函数的图象与性质解决实际问题,是一道综合题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
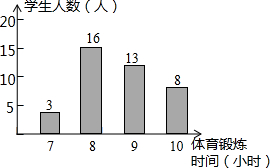 (2013•大丰市二模)为了了解“阳光体育运动”的实施情况,将某校40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,则该校40名同学一周参加体育锻炼时间的中位数是( )
(2013•大丰市二模)为了了解“阳光体育运动”的实施情况,将某校40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,则该校40名同学一周参加体育锻炼时间的中位数是( )
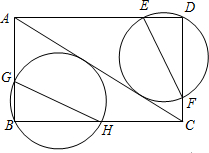 (2013•大丰市二模)如图,在矩形ABCD中,BC=8,AB=6,经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是
(2013•大丰市二模)如图,在矩形ABCD中,BC=8,AB=6,经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是