题目内容
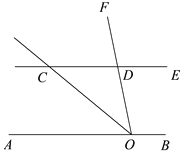
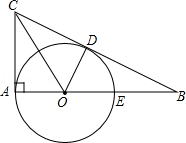
【题目】如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B 
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为3cm,求 ![]() 的长度(结果保留π)
的长度(结果保留π)
【答案】
(1)证明:∵AC是⊙O切线,
∴OA⊥AC,
∴∠OAC=90°,
∵CO平分∠AOD,
∴∠AOC=∠COD,
在△AOC和△DOC中,
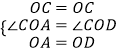 ,
,
∴△AOC≌△DOC,
∴∠ODC=∠OAC=90°,
∴OD⊥CD,
∴直线CD是⊙O的切线
(2)解:∵OD⊥BC,DC=DB,
∴OC=OB,
∴∠OCD=∠B=∠ACO,
∵∠B+∠ACB=90°,
∴∠B=30°,∠DOE=60°,
∴ ![]() 的长=
的长= ![]() =π.
=π.
【解析】(1)欲证明直线CD是⊙O的切线,只要证明∠ODC=90°即可.(2)先证明∠B=∠OCB=∠ACO,推出∠B=30°,∠DOE=60°,利用弧长公式即可解决问题.

练习册系列答案
相关题目
【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.