Question

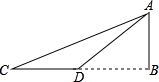如图，河岸边有座水塔AB，测量人员在河对岸C处测得塔顶A的仰角为30°，然后沿着CB方向前进30米到达D处，又测得A的仰角为45°，请根据上述数据计算水塔的高（结果精确到0.1，

2

≈1.414，

3

≈1.732）．

Answer 1

分析：利用AB表示出BC，BD．让BC减去BD等于30即可求得AB长．

解答：解：设AB=x．
则BC=AB÷tan∠ACB=

3

x，BD=AB÷tan∠ADB=x．
则CD=BC-BD=（

3

-1）x=30．
解可得：x=AB=

30

3 -1

=15（

3

+1），
则AB≈41.0（米）．
答：水塔高41.0米．

点评：本题主要考查了三角函数的定义，根据三角函数可以把问题转化为方程问题来解决．