题目内容
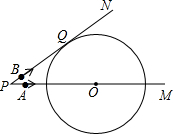如图，已知⊙O的半径为6cm，射线PM经过点O，OP=10cm，射线PN与⊙O相切于点Q，A，B两点同时从点P出发，点A以5cm/s的速度沿射线PM方向运动，点B以4cm/s的速度沿射线PN方向运动．设运动时间为t（s）．当直线AB与⊙O相切时，t（s）的值是（ ）| A、0.5 | B、3.5 | C、0.5或2.5 | D、0.5或3.5 |
练习册系列答案
相关题目
如图，已知AB是⊙O的直径，C、D是⊙O上的两点，∠BAC=20°， |
| AD |
|
| DC |
| A、30° | B、35° |
| C、45° | D、70° |
如图，Rt△ABC中，∠ACB=90°，AC=4，BC=6，以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E，则AD为（ ）| A、2.5 | B、1.6 | C、1.5 | D、1 |
如图，已知AB是⊙O的直径，C是AB延长线上一点，BC=OB，CE是⊙O的切线，切点为D，过点A作AE⊥CE，垂足为E，则DE：AE的值是（ ）
如图，在Rt△AOB中，OA=OB=3
如图，AB是⊙O的直径，CD是⊙O的切线，C为切点，∠D=40°，则∠B等于（ ）| A、15° | B、20° | C、25° | D、30° |
如图，扇形AOD中，∠AOD=90°，OA=6，点P为 |
| AD |
|
| AD |
| A、0＜r＜3 | ||
| B、r=3 | ||
C、3＜r＜3
| ||
D、r=3
|
已知⊙O1的半径是5cm，⊙O2的半径是3cm，O1O2=6cm，则⊙O1和⊙O2的位置关系是（ ）
| A、相交 | B、外切 | C、外离 | D、内含 |
一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形，边长都为1，则扇形和圆形纸板的面积比是（ ）| A、5：4 | ||||
| B、5：2 | ||||
C、
| ||||
D、
|