题目内容
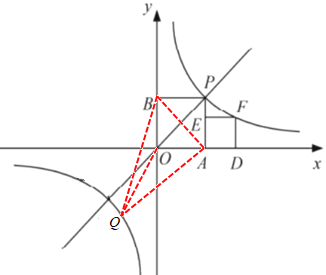
【题目】如图,正方形OAPB、ADFE的顶点A、D. B在坐标轴上,点B在AP上,点P、F在函数![]() 上,已知正方形OAPB的面积是9.
上,已知正方形OAPB的面积是9.

(1)求k的值和直线OP的解析式;
(2)求正方形ADFE的边长
(3)函数![]() 在第三象限的图像上是否存在一点Q,使得△ABQ的面积为10.5?若存在,求出Q点坐标;若不存在,请说明理由.
在第三象限的图像上是否存在一点Q,使得△ABQ的面积为10.5?若存在,求出Q点坐标;若不存在,请说明理由.
【答案】(1)![]() ;直线OP的解析式为y=x;(2)正方形ADFE的边长为得
;直线OP的解析式为y=x;(2)正方形ADFE的边长为得![]() ;(3)不存在.
;(3)不存在.
【解析】
(1)利用正方形的性质得到P点坐标为(3,3),再把P点坐标代入![]() 即可得到k的值;然后利用待定系数法求直线OP的解析式;
即可得到k的值;然后利用待定系数法求直线OP的解析式;
(2)设正方形ADFE的边长为a,利用正方形的性质易表示F点的坐标为(a+3,a),然后把F(a+3,a)代入![]() ,再解关于a的一元二次方程即可得到正方形ADFE的边长;
,再解关于a的一元二次方程即可得到正方形ADFE的边长;
(3)如图,连接QA,QB,QO,AB,设Q(x,y)(x<0),利用S△ABQ=S△AOQ+ S△BOQ+ S△ABO=10.5列出关于x的方程求解即可.
(1)∵正方形OAPB的面积为9,
∴PA=PB=3,
∴P点坐标为(3,3),
把P(3,3)代入![]() 得,k=3×3=9,
得,k=3×3=9,
即![]() ;
;
设直线OP的解析式为y=k1x,
把P(3,3)代入y=k1x得,k1=1,
∴直线OP的解析式为y=x;
(2)设正方形ADFE的边长为a,则F点的坐标为(a+3,a),
把F(a+3,a)代入![]() 得,a(a+3)=9,解得a1=
得,a(a+3)=9,解得a1=![]() ,a2=
,a2=![]() ,
,
∴正方形ADFE的边长为得![]() ;
;
(3)∵P(3,3)且四边形AOBP是正方形,
∴AO=BO=3,
设Q(x,![]() )(x<0),连接QO,QB,QA,AB,如图所示,
)(x<0),连接QO,QB,QA,AB,如图所示,
假定△ABQ的面积为10.5,则有,
S△BOQ+S△AOQ+S△AOB=10.5
即,![]()
∵x<0
∴方程整理得,![]()
∵△=![]()
∴此方程无实数解,
故函数![]() 在第三象限的图像上不存在一点Q,使得△ABQ的面积为10.5
在第三象限的图像上不存在一点Q,使得△ABQ的面积为10.5

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案