题目内容
一只不透明的袋子中,装有3个白球和1个红球,这些球除颜色外都相同.(1)小明认为,搅均后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球的概率相同.你同意他的说法吗?为什么?
(2)搅均后从中一把摸出两个球,请通过列表或树状图求两个球都是白球的概率;
(3)小明往该口袋中又放入红球和白球若干个,一段时间后他记不清具体放入红球和白球的个数,只记得一种球的个数比另一种球的个数多1,且从口袋中取出一个白球的概率为
| 2 | 3 |
分析:(1)求出分别摸到白球与摸到红球的概率,比较这两个概率,即可知道谁的可能性大,概率大则可能性就大;
(2)考查了树状图法或者列表法求概率,解题时要注意此题为不放回实验;
(3)此题考查了借助方程思想求概率的问题,解题的关键是找到等量关系,注意分放入白球的个数比红球的个数多1;放入红球的个数比白球的个数多1两种情况讨论.
(2)考查了树状图法或者列表法求概率,解题时要注意此题为不放回实验;
(3)此题考查了借助方程思想求概率的问题,解题的关键是找到等量关系,注意分放入白球的个数比红球的个数多1;放入红球的个数比白球的个数多1两种情况讨论.
解答:解:(1)不同意小明的说法,因为摸出白球的概率是
,摸出红球的概率是
,因此摸出白球和摸出红球不是等可能的;
(2)列表得:
∴一共有12种情况,两个球都是白球的有6种情况,
∴P(两个球都是白球)=
=
;
(3)①设应添加x个红球,添加(x+1)个白球,由题意得
=
,
解得x=2(经检验是原方程的解),
x+1=3.
故应添加2个红球,添加3个白球;
②设应添加x个白球,添加(x+1)个红球,由题意得
=
,
解得x=-1(不合题意,舍去).
综上可知应添加2个红球,添加3个白球.
| 3 |
| 4 |
| 1 |
| 4 |
(2)列表得:
| ( 白1,白2) | (白1,白3) | (白1,红) |
| (白2,白1) | (白2,白3) | (白2,红) |
| (白3,白1) | (白3,白2) | (白3,红) |
| (红,白1) | (红,白2) | (红,白3) |
∴P(两个球都是白球)=
| 6 |
| 12 |
| 1 |
| 2 |
(3)①设应添加x个红球,添加(x+1)个白球,由题意得
| 3+x+1 |
| 3+x+1+1+x |
| 2 |
| 3 |
解得x=2(经检验是原方程的解),
x+1=3.
故应添加2个红球,添加3个白球;
②设应添加x个白球,添加(x+1)个红球,由题意得
| 3+x |
| 3+x+1+x+1 |
| 2 |
| 3 |
解得x=-1(不合题意,舍去).
综上可知应添加2个红球,添加3个白球.
点评:本题考查了学生对概率问题的理解,要注意方程思想的应用;还考查了用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3、4、5、x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是 .
(2)如果摸出的这两个小球上数字之和为9的概率是
,那么x的值可以取7吗?请用列表法或画树状图法说明理由;如果x的值不可以取7,请写出一个符合要求的x值.
| 摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为8”出现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为8”出现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是
(2)如果摸出的这两个小球上数字之和为9的概率是
| 1 |
| 3 |
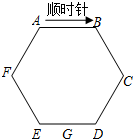 一枚棋子放在边长为1个单位长度的正六边形ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位长度.
一枚棋子放在边长为1个单位长度的正六边形ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位长度.