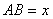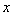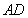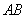题目内容
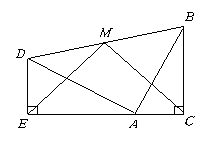
两个全等的含300， 600角的三角板ADE和三角板ABC如图所示放置，E，A，C三点在一条直线上，连结BD，取BD的中点M，连结ME，MC。试判断△EMC的形状，并说明理由。
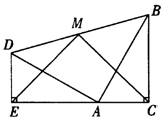
解：△EMC是等腰直角三角形。
证明：由题意，得
DE=AC，∠DAE＋∠BAC=900，
∴∠DAB=900。
连接AM．∵DM=MB
∴MA=
DB=DM，∠MDA=∠MAB=450.
∴∠MDE=∠MAC=1050
∴△EDM≌△CAM
∴EM=MC， ∠DME=∠AMC
又∠EMC=∠EMA+∠AMC=∠EMA+∠DME=900
∴CM⊥EM
所以△EMC是等腰直角三角形
练习册系列答案
相关题目
