Question

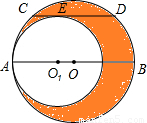
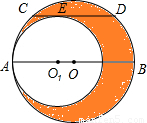
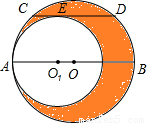
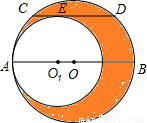
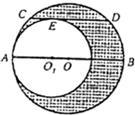22、如图所示，大圆O与小圆O₁相切于点A，大圆的弦CD与小圆相切于点E，且CD∥AB，若CD=2cm，则阴影部分的面积S_阴影=

π

cm²．

Answer 1

分析：过O作OF⊥CD，垂足为F，连接OC，由垂径定理知点F是CD的中点，即CF=1；再由CD∥AB知道OF等于小圆的半径的长，OC是大圆的半径，然后根据S_阴影部分=S_大圆-S_小圆=π（OE²-OF²）=π•CF²即可求出其结果．

解答：解：如图，连接O₁E，作OF⊥CD，垂足为F，连接OC，
∵大圆的弦CD与小圆相切于点E，
∴O₁E⊥CD，
由垂径定理知，点F是CD的中点，
而CD=2cm，
∴CF=1；
∵CD∥AB，
∴OF等于小圆的半径的长，OC是大圆的半径，
∴S_阴影部分=S_大圆-S_小圆=π（OC²-OF²）=π•CF²=π．

故填空答案：π．

点评：本题利用了圆的面积公式，两平行线CD与AB之间的距离是定值求解．