题目内容
把多项式x2-11x+24分解因式,可以采取以下两种方法:①将-11x拆成两项,-6x-5x;将24拆成两项,9+15,则:x2-11x+24=x2-6x+9-5x+15=(x2-6x+9)-5(x-3)=(x-3)2-5(x-3)=(x-3)[(x-3)-5]=(x-3)(x-8).
②添加一个数(
| 11 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
| 25 |
| 4 |
| 11 |
| 2 |
| 5 |
| 2 |
| 11 |
| 2 |
| 5 |
| 2 |
| 11 |
| 2 |
| 5 |
| 2 |
根据上面的启发,请将多项式x2+4x-12分解因式.
分析:根据完全平方公式的特点拆-12=4-16,再根据平方差公式分解即可.
解答:解:x2+4x-12
=x2+4x+4-16
=(x+2)2-16
=(x+2-4)(x+2+4)
=(x-2)(x+6).
=x2+4x+4-16
=(x+2)2-16
=(x+2-4)(x+2+4)
=(x-2)(x+6).
点评:本题主要考查对分解因式的方法的理解和掌握,能熟练地运用公式分解因式是解此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
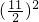 ,再减去这个数
,再减去这个数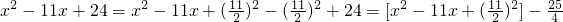 =
=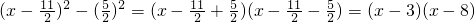 .
.