题目内容
25、证明:等腰三角形中,底边上的高线、中线、顶角的平分线重合.
分析:分AD是BC边上的高;AD是BC边的中线;AD平分∠BAC三种情况讨论,通过证明三角形全等得以证明.
解答: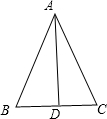 解:1、已知三角形ABC中,AB=AC,AD是BC边上的高.求证:BD=CD,∠BAD=∠CAD.
解:1、已知三角形ABC中,AB=AC,AD是BC边上的高.求证:BD=CD,∠BAD=∠CAD.
证明:因为AD是高,所以∠ADB=∠ADC=90度,
因为AB=AC,AD=AD,
所以直角△ABD全等直角△ACD(HL)
所以BD=CD,∠BAD=∠CAD.
2、已知三角形ABC中,AB=AC,AD是BC边的中线,求证:AD⊥BC,∠BAD=∠CAD.
证明:因为AB=AC,AD=AD,BD=CD,
所以△ABD≌△ACD,
所以∠ADB=∠ADC,∠BAD=∠CAD.
因为∠ADB+∠ADC=180度,
所以∠ADB=90度,即有AD⊥BC.
3、已知三角形ABC中,AB=AC,AD平分∠BAC,求证:AD⊥BC,BD=CD.
证明:因为AB=AC,∠BAD=∠CAD,AD=AD,
所以△ABD≌△ACD,
所以∠ADB=∠ADC,BD=CD,
因为∠ADB+∠ADC=180度,
所以∠ADB=90度,即有AD⊥BC.
 解:1、已知三角形ABC中,AB=AC,AD是BC边上的高.求证:BD=CD,∠BAD=∠CAD.
解:1、已知三角形ABC中,AB=AC,AD是BC边上的高.求证:BD=CD,∠BAD=∠CAD.证明:因为AD是高,所以∠ADB=∠ADC=90度,
因为AB=AC,AD=AD,
所以直角△ABD全等直角△ACD(HL)
所以BD=CD,∠BAD=∠CAD.
2、已知三角形ABC中,AB=AC,AD是BC边的中线,求证:AD⊥BC,∠BAD=∠CAD.
证明:因为AB=AC,AD=AD,BD=CD,
所以△ABD≌△ACD,
所以∠ADB=∠ADC,∠BAD=∠CAD.
因为∠ADB+∠ADC=180度,
所以∠ADB=90度,即有AD⊥BC.
3、已知三角形ABC中,AB=AC,AD平分∠BAC,求证:AD⊥BC,BD=CD.
证明:因为AB=AC,∠BAD=∠CAD,AD=AD,
所以△ABD≌△ACD,
所以∠ADB=∠ADC,BD=CD,
因为∠ADB+∠ADC=180度,
所以∠ADB=90度,即有AD⊥BC.
点评:本题考查了等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合,即三线合一的证明.注意分类思想的运用.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目