题目内容
如图,在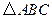 中,
中, ,
,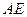 是角平分线,
是角平分线,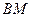 平分
平分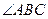 交
交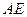 于
于点
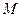 ,经过
,经过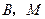 两点的
两点的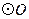 交
交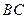 于点
于点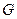 ,交
,交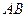 于点
于点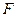 ,
,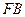 恰为
恰为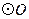 的直径.
的直径.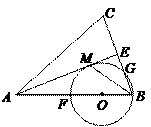
(1)求证:
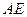 与
与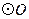 相切;
相切;(2)当
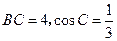 时,求
时,求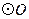 的半径.
的半径.
解:(1)证明:连结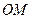 ,则
,则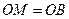 .
.

∴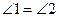 .
.
∵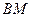 平分
平分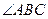 .
.
∴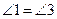 .
.
∴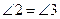 .
.
∴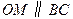 .
.
∴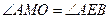 .…………………………..1分
.…………………………..1分
在 中,
中,
∵ ,
,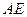 是角平分线,
是角平分线,
∴ .………………………………………………………………………..….2分
.………………………………………………………………………..….2分
∴ .
.
∴ .
.
∴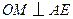 .
.
∴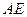 与
与 相切.………………………………………………………………………3分
相切.………………………………………………………………………3分
(2)解:在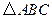 中,
中, ,
,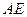 是角平分线,
是角平分线,
∴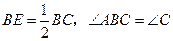 .
.
∵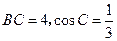 ,
,
∴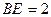 ,
,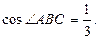
在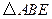 中,
中, ,
,
∴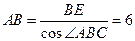 .………………………………………………………………….4分
.………………………………………………………………….4分
设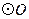 的半径为
的半径为 ,则
,则 .
.
∵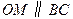 ,
,
∴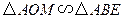 .
.
∴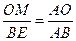 .
.
∴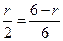 .
.
解得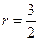 .∴
.∴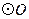 的半径为
的半径为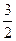 .………………………………………………………….5分解析:
.………………………………………………………….5分解析:
略
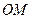 ,则
,则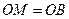 .
.
∴
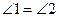 .
.∵
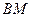 平分
平分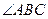 .
.∴
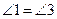 .
.∴
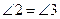 .
.∴
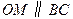 .
.∴
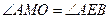 .…………………………..1分
.…………………………..1分在
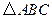 中,
中,∵
 ,
,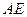 是角平分线,
是角平分线,∴
 .………………………………………………………………………..….2分
.………………………………………………………………………..….2分∴
 .
.∴
 .
.∴
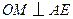 .
.∴
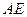 与
与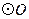 相切.………………………………………………………………………3分
相切.………………………………………………………………………3分(2)解:在
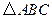 中,
中, ,
,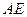 是角平分线,
是角平分线,∴
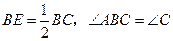 .
.∵
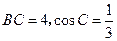 ,
,∴
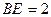 ,
,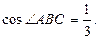
在
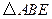 中,
中, ,
,∴
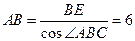 .………………………………………………………………….4分
.………………………………………………………………….4分设
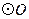 的半径为
的半径为 ,则
,则 .
.∵
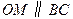 ,
,∴
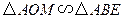 .
.∴
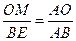 .
.∴
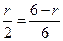 .
.解得
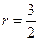 .∴
.∴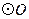 的半径为
的半径为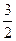 .………………………………………………………….5分解析:
.………………………………………………………….5分解析:略

练习册系列答案
相关题目
 16、如图,在△ABC中,AD是△ABC中∠CAB的角平分钱,要使△ADC≌△ADE,需要添加一个条件,这个条件是
16、如图,在△ABC中,AD是△ABC中∠CAB的角平分钱,要使△ADC≌△ADE,需要添加一个条件,这个条件是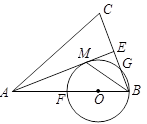
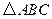 中,
中,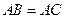 ,
,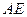 是角平分线,
是角平分线, 平分
平分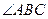 交
交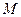 ,经过
,经过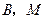 两点的
两点的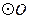 交
交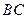 于点
于点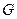 ,交
,交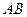 于点
于点 ,
,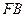 恰为
恰为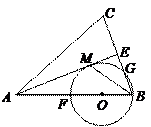
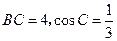 时,求
时,求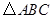 中,
中,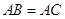 ,
, 是角平分线,
是角平分线,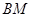 平分
平分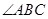 交
交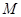 ,经过
,经过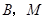 两点的
两点的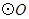 交
交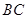 于点
于点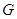 ,交
,交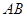 于点
于点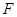 ,
,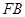 恰为
恰为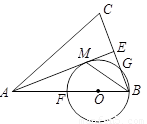
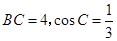 时,求
时,求