题目内容
(2003•资阳)如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E.(1)求证:BC∥DE;
(2)若AB=3,BD=2,求CE的长;
(3)在题设条件下,为使BDEC是平行四边形,△ABC应满足怎样的条件(不要求证明).
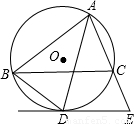
【答案】分析:(1)连接CD,可根据圆周角定理通过AD平分∠BAC得出∠DCB=∠DBC,根据弦切角定理可得出∠CDE=∠DBC,将等角置换后即可得出∠BCD=∠CDE.即可得出平行;
(2)由(1)不难得出BD=CD(等角对等边),然后通过证明三角形ABD和CDE相似,来得出AB、BC、CD、CE的比例关系,有了AB、BD、CD的值就求出了CE的长;
(3)要使BDEC是平行四边形,那么BD∥CE,可通过弦切角定理得出∠BAD=∠ACB,也就得出了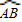 =
=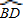 ,上面(1)中已经得出
,上面(1)中已经得出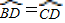 ,因此
,因此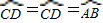 ,∠ACB=∠BAD=∠CAD,因此∠BAC=2∠ACB.
,∠ACB=∠BAD=∠CAD,因此∠BAC=2∠ACB.
解答: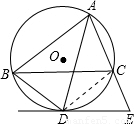 (1)证明:连接CD;
(1)证明:连接CD;
∵DE是圆O的切线,
∴∠CDE=∠CBD.
∵∠CBD=∠DAC,
∴∠CDE=∠DAC.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∴∠CDE=∠BAD.
∵∠BAD=∠BCD,
∴∠CDE=∠BCD.
∴BC∥DE.
(2)解:如图,连接CD;
∵AD平分∠BAC,
∴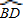 =
=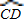 .
.
∴∠BCD=∠CBD.
∴BD=CD=2.
∵BC∥DE,
∴∠E=∠ACB=∠ADB.
又由(1)中已证得∠CDE=∠BAD,
∴△ABD∽△DCE.
∴AB:BD=CD:CE.
∴CE=BD•CD÷AB= .
.
(3)解:应该是∠BAC=2∠ACB.
点评:本题主要考查了切线的性质,相似三角形的判定和应用等知识点,有一定的综合性.
(2)由(1)不难得出BD=CD(等角对等边),然后通过证明三角形ABD和CDE相似,来得出AB、BC、CD、CE的比例关系,有了AB、BD、CD的值就求出了CE的长;
(3)要使BDEC是平行四边形,那么BD∥CE,可通过弦切角定理得出∠BAD=∠ACB,也就得出了
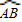 =
=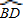 ,上面(1)中已经得出
,上面(1)中已经得出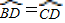 ,因此
,因此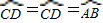 ,∠ACB=∠BAD=∠CAD,因此∠BAC=2∠ACB.
,∠ACB=∠BAD=∠CAD,因此∠BAC=2∠ACB.解答:
 (1)证明:连接CD;
(1)证明:连接CD;∵DE是圆O的切线,
∴∠CDE=∠CBD.
∵∠CBD=∠DAC,
∴∠CDE=∠DAC.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∴∠CDE=∠BAD.
∵∠BAD=∠BCD,
∴∠CDE=∠BCD.
∴BC∥DE.
(2)解:如图,连接CD;
∵AD平分∠BAC,
∴
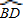 =
=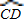 .
.∴∠BCD=∠CBD.
∴BD=CD=2.
∵BC∥DE,
∴∠E=∠ACB=∠ADB.
又由(1)中已证得∠CDE=∠BAD,
∴△ABD∽△DCE.
∴AB:BD=CD:CE.
∴CE=BD•CD÷AB=
 .
.(3)解:应该是∠BAC=2∠ACB.
点评:本题主要考查了切线的性质,相似三角形的判定和应用等知识点,有一定的综合性.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
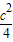 ,其中a、b、c分别是△ABC中∠A、∠B、∠C所对边的长.
,其中a、b、c分别是△ABC中∠A、∠B、∠C所对边的长.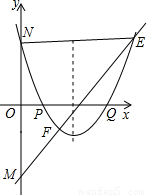
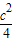 ,其中a、b、c分别是△ABC中∠A、∠B、∠C所对边的长.
,其中a、b、c分别是△ABC中∠A、∠B、∠C所对边的长.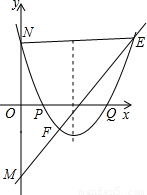
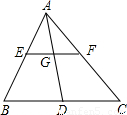
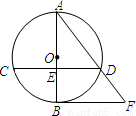
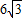 ,BD=3.
,BD=3.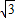 ,BD=3,∴
,BD=3,∴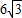 =AB cosA=(AD+BD)cosA=(
=AB cosA=(AD+BD)cosA=(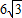 cosA+3)cosA,设t=cosA,则t>0,且上式可化为
cosA+3)cosA,设t=cosA,则t>0,且上式可化为 t2+______
t2+______