题目内容
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为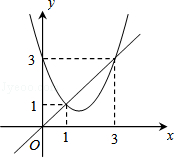
| A.1 | B.2 | C.3 | D.4 |
B
解析分析:∵函数y=x2+bx+c与x轴无交点,∴b2﹣4c<0;故①错误。
当x=1时,y=1+b+c=1,故②错误。
∵当x=3时,y=9+3b+c=3,∴3b+c+6=0。故③正确。
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,∴x2+(b﹣1)x+c<0。故④正确。
综上所述,正确的结论有③④两个,故选B。

练习册系列答案
相关题目
已知二次函数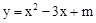 (m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程
(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程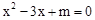 的两实数根是
的两实数根是
| A.x1=1,x2=-1 | B.x1=1,x2=2 |
| C.x1=1,x2=0 | D.x1=1,x2=3 |
二次函数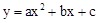 的图象如图所示,反比例函数
的图象如图所示,反比例函数 与一次函数
与一次函数 在同一平面直角坐标系中的大致图象是
在同一平面直角坐标系中的大致图象是
A. | B. | C. | D. |
下列二次函数的图象,不能通过函数y=3x2的图象平移得到的是
| A.y=3x2+2 | B.y=3(x﹣1)2 |
| C.y=3(x﹣1)2+2 | D.y=2x2 |
抛物线y=ax2+bx+c(a<0)如图所示,则关于x的不等式ax2+bx+c>0的解集是
| A.x<2 | B.x>﹣3 | C.﹣3<x<1 | D.x<﹣3或x>1 |
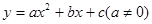 的图象经过点
的图象经过点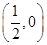 ,对称轴为直线
,对称轴为直线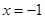 ,下列5个结论:①
,下列5个结论:① ; ②
; ② ; ③
; ③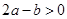 ;④
;④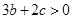 ; ⑤
; ⑤ ,
,
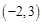 ,并且经过平移后能与抛物线
,并且经过平移后能与抛物线 重合,那么这个二次函数的解析式是 .
重合,那么这个二次函数的解析式是 .