Question

等腰梯形的中位线长为m，且对角线互相垂直，求梯形的高和面积．

Answer 1

答案：
解析：

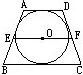
解：如图，等腰梯形ABCD中，AB∥CD，EF是中位线，对角线AC⊥BD于O． 　　过C作DB的平行线交AB的延长线于G点，作CH⊥AB于H，则四边形DCGB是平行四边形． 　　∴BG＝CD，BD＝CG． 　　∵BD⊥AC于O， 　　∴CG⊥AC，即∠ACG＝． 　　又∵四边形ABCD是等腰梯形， 　　∴AC＝BD＝CG． 　　∴H是AG的中点． 　　∴CH＝AG＝(AB＋BG) 　　＝(AB＋CD)＝EF． 　　∴梯形的高CH＝EF＝m， 　　梯形的面积EF·CH＝m2．

提示：

点悟：梯形的面积等于中位线与高的乘积，应添加辅助线，使梯形的对角线与“两底”集中到同一个三角形中，从而解决问题．